<span style="font-size: 16pt; color: blue">拾人牙慧</span>

如何移值 ssh private key 到別台機器上？
在原本的機器上，已經有 ssh private key，並以此 private key 產生 public key，並以此 public key 取得授權後，如何把 private key 移植到新的機器上？

Tera Term Macro 簡易範例



Tera Term Macro 的副檔名為 .ttl，而 ttl stands for Tera Term Language，以下為簡易範例。


; 變數 i，初始值為 1
i = 1

; 執行迴圈，以變數 i 來控制
do while i<=1000

; 等待畫面出現 login 字串
wait 'xxx login:'

; 顯示另一個小視窗，內容為 i 的值
statusbox i 'test_count'

; 輸入帳號 - "id"
sendln 'ID'

; 等待 1 秒
pause 1

; 輸入密碼 - "password"
sendln 'PASSWORD'

; 等待 5 秒
pause 5

; 把 i 值作輸入，讓 i 的變數值可以被紀錄在 console 上
msg='test_count:'
msg2=''
int2str msg2 i
strconcat msg msg2
sendln msg

; 執行 date 指令
sendln 'date'

; 執行 reboot 指令
sendln 'reboot'

pause 5

; 增加變數 i 的值
i=i+1
loop



Reference



TTL command reference

RSA 加密與解密



RSA 為非對稱式加密，也就是說用來加密的鑰匙 跟 用來解密的鑰匙 是不相同的。

用來加密的鑰匙稱為公鑰，公鑰是可以公開的，任何人有了公鑰後，可以對明文訊息以公鑰加密後變成密文，傳送給接收方。

用來解密的鑰匙稱為私鑰，接收方收到密文後，可以利用私鑰來解密，得到明文訊息。

其它人就算得到密文，也因為沒有私鑰，所以無法將密文解密。



本文分成以下數個部分：

RSA 的加密與解密方式

RSA 的公鑰及私鑰

RSA 的解密原理

RSA 的加密與解密範例





RSA 的加密與解密方式



RSA 加密與解密方式為：公鑰加密，私鑰解密

公鑰： e, n

私鑰： d, n

訊息： m

密文： c



將 m 加密，得到密文 c，加密方式為：

m^e ≡ c (mod n)

對 m 的 e 次方 取 n 的餘數，所得值為 c。



將 c 解密，得到明文 m，解密方式為：

c^d ≡ m (mod n)

對 c 的 d 次方 取 n 的餘數，所得值為 m。



從上述加、解密方式可以知道，公鑰及私鑰不能是隨便產生的，必須遵循它的規則，否則上述算式將不會成立。





RSA 的公鑰及私鑰



要計算 RSA 的公鑰及私鑰，得先從決定 n 的值開始。

選擇兩個質數 p 及 q，令 n = p x q。

令 f(n) 為與 n 互值且小於 n 的整數個數，根據 歐拉定理 f(n) = (p-1) x (q-1)。



決定公鑰 e 的值，條件為： e 與 f(n) 互質，且 1 < e < f(n)。

決定私鑰 d 的值，條件為： 使得 d x e ≡ 1 (mod f(n)) 成立。



如此公鑰及私鑰都已經決定完成。





RSA 的解密原理



解密的方式為：

c^d ≡ m (mod n)

所以要証明上述加、解密可以運作順利，就要証明上式成立。

因為加密方式為：

m^e ≡ c (mod n)

所以：

c = m^e - kn

代入解密方式：

(m^e - kn)^d ≡ m (mod n)

又因為 kn 一定是 n 的倍數，mod n 的值為 0，所以上式可以簡化為：

(m^e)^d ≡ m (mod n)

=> m^ed ≡ m (mod n)

又因為：

d x e ≡ 1 (mod f(n))

所以：

d x e = h f(n) + 1

代入原式，可以得到：

m^ed = m^{h f(n) + 1} ≡ m (mod n)

接下來分成兩種情況：



第一種： m 與 n 互質，則根據歐拉定理：

m^f(n) ≡ 1 (mod n)

所以原式成為：

m^{h f(n) + 1} = [(m^f(n))^h] x m = 1 x m = m ≡ m (mod n)

=> 則原式成立。



第二種： m 與 n 不互質

因為 n = p x q，且 p, q 為質數，所以 m 一定為 k x p 或 k x q。

以 m = kp 為例，又因為 q 是質數，且 m < n = p x q，所以 k 與 q 一定是互質，則根據歐拉定理：

(kp)^q-1 ≡ 1 (mod q)

所以下式也會成立：

[(kp)^q-1]^h(p-1) x kp ≡ kp (mod q)

=> (kp)^{(q-1) x (h(p-1))} x kp ≡ kp (mod q)

又因為：

d x e = h f(n) + 1

所以：

(kp)^{(q-1) x (h(p-1))} x kp = (kp)^{h(q-1)(p-1)+1} = (kp)^ed ≡ kp (mod q)

把 kp (mod q) 展開，可以寫成：

(kp)^ed = tq + kp

又因為 (kp)^ed 一定是 p 的位數，所以 (tq + kp) 也一定是 p 的倍數，所以 tq 一定也是 p 的倍數，又 p 與 q 互值，所以 t 一定是 p 的位數，所以：

(kp)^ed = tq + kp = t'pq + kp

又因為 m = kp 且 n = pq，代入上式後，得到：

m^ed = t'n + m ≡ m (mod n)

=> 原式成立。





RSA 的加密與解密範例



公鑰： e, n

私鑰： d, n

訊息： m

密文： c



取 p = 3、q = 11，所以 n = 33。

f(n) = (3-1)(11-1) = 20。

又條件為：

ed ≡ 1 (mod 20)

ed = 20k + 1，取 k = 1，令 e = 3、d = 7。

所以公鑰為： (3, 33)，私鑰為： (7, 33)。



假設訊息為 m = 17

加密： (17)³ (mod 33) = 29



密文 c = 29

解密： (29)⁷ (mod 33) = 17





Reference



輕鬆學習RSA加密演算法原理



RSA算法原理（二）

shell script 筆紀
如果要查詢 shell script 的寫法，可以利用 $ man bash 指令，內容很詳細，幾乎所有的用法都可以找到。

table td, table th {padding: 6px; border:1px solid #000000;}

table td, table th {padding: 6px; border:1px solid #000000;}
理解 lspci
在 linux 中，可以利用 lspci 指令來列出所有連接的 PCI 裝置，本文簡單說明 lspci 的顯示結果。
lspci 的顯示結果
以 Interpreting the output of lspci 的例子來說：

table td, table th {padding: 6px; border:1px solid #000000;}

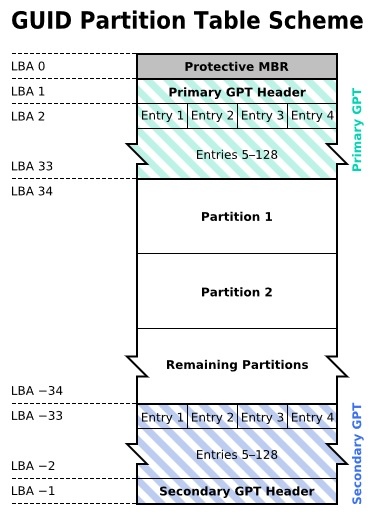
table td, table th {padding: 6px; border:1px solid #000000;}
GUID Partition Table (GPT)
GPT 是一個實體硬碟的分割區表的結構布局的標準。它是可延伸韌體介面（UEFI）標準的一部分，被用於替代 BIOS 系統中的一 32bits 來儲存邏輯塊位址和大小資訊的主開機紀錄（Master Boot Record, MBR）分割區表。
在 Embedded System 中，通常會把 UFS(Universal Flash Storage) 切割成好幾個 LUN(Logical Unit Number)，每個 LUN 可以視為一個虛擬硬碟，也就是說每個 LUN 都會有自己的 GPT，又每個 GPT 最多只能紀錄 128 Entries，所以每個 LUN 中，最多可以存在 128 個 Partitions，而每個 Partition 都會有自己的 Partition Entry。
GPT 的結構
在 MBR 硬碟中，分割區資訊直接儲存於主開機紀錄（MBR）中（主開機紀錄中還儲存著系統的啟動程式）。但在 GPT 硬碟中，分割區表的位置資訊儲存在 GPT Header 中。只是出於相容性考慮，硬碟的第一個磁區仍然用作 MBR，之後才是 GPT Header。
跟現代的 MBR 一樣，GPT 也使用邏輯區塊位址（Logical Block Addressing, LBA）取代了早期的 CHS 尋址方式。傳統 MBR 資訊儲存於 LBA 0，GPT Header 儲存於LBA 1，接下來才是 Partition Entry。在上圖的例子中，每個 LBA 為 512 bytes，每個 Partition Entry 的記錄為 128 bytes。
而為了減少分割區表損壞的風險，GPT 在硬碟最後儲存了一份分割區表的副本。
GPT 的資料結構
GPT Header 的資料結構
佔 512 bytes

table td, table th {padding: 6px; border:1px solid #000000;}

table td, table th {padding: 6px; border:1px solid #000000;}