<span style="font-size: 16pt; color: blue">拾人牙慧</span>

table td, table th {padding: 6px; border:1px solid #000000;}
相機感光元件 - Bayer Sensor
感光元件

Tera Term Macro 簡易範例



Tera Term Macro 的副檔名為 .ttl，而 ttl stands for Tera Term Language，以下為簡易範例。


; 變數 i，初始值為 1
i = 1

; 執行迴圈，以變數 i 來控制
do while i<=1000

; 等待畫面出現 login 字串
wait 'xxx login:'

; 顯示另一個小視窗，內容為 i 的值
statusbox i 'test_count'

; 輸入帳號 - "id"
sendln 'ID'

; 等待 1 秒
pause 1

; 輸入密碼 - "password"
sendln 'PASSWORD'

; 等待 5 秒
pause 5

; 把 i 值作輸入，讓 i 的變數值可以被紀錄在 console 上
msg='test_count:'
msg2=''
int2str msg2 i
strconcat msg msg2
sendln msg

; 執行 date 指令
sendln 'date'

; 執行 reboot 指令
sendln 'reboot'

pause 5

; 增加變數 i 的值
i=i+1
loop



Reference



TTL command reference

RSA 加密與解密



RSA 為非對稱式加密，也就是說用來加密的鑰匙 跟 用來解密的鑰匙 是不相同的。

用來加密的鑰匙稱為公鑰，公鑰是可以公開的，任何人有了公鑰後，可以對明文訊息以公鑰加密後變成密文，傳送給接收方。

用來解密的鑰匙稱為私鑰，接收方收到密文後，可以利用私鑰來解密，得到明文訊息。

其它人就算得到密文，也因為沒有私鑰，所以無法將密文解密。



本文分成以下數個部分：

RSA 的加密與解密方式

RSA 的公鑰及私鑰

RSA 的解密原理

RSA 的加密與解密範例





RSA 的加密與解密方式



RSA 加密與解密方式為：公鑰加密，私鑰解密

公鑰： e, n

私鑰： d, n

訊息： m

密文： c



將 m 加密，得到密文 c，加密方式為：

m^e ≡ c (mod n)

對 m 的 e 次方 取 n 的餘數，所得值為 c。



將 c 解密，得到明文 m，解密方式為：

c^d ≡ m (mod n)

對 c 的 d 次方 取 n 的餘數，所得值為 m。



從上述加、解密方式可以知道，公鑰及私鑰不能是隨便產生的，必須遵循它的規則，否則上述算式將不會成立。





RSA 的公鑰及私鑰



要計算 RSA 的公鑰及私鑰，得先從決定 n 的值開始。

選擇兩個質數 p 及 q，令 n = p x q。

令 f(n) 為與 n 互值且小於 n 的整數個數，根據 歐拉定理 f(n) = (p-1) x (q-1)。



決定公鑰 e 的值，條件為： e 與 f(n) 互質，且 1 < e < f(n)。

決定私鑰 d 的值，條件為： 使得 d x e ≡ 1 (mod f(n)) 成立。



如此公鑰及私鑰都已經決定完成。





RSA 的解密原理



解密的方式為：

c^d ≡ m (mod n)

所以要証明上述加、解密可以運作順利，就要証明上式成立。

因為加密方式為：

m^e ≡ c (mod n)

所以：

c = m^e - kn

代入解密方式：

(m^e - kn)^d ≡ m (mod n)

又因為 kn 一定是 n 的倍數，mod n 的值為 0，所以上式可以簡化為：

(m^e)^d ≡ m (mod n)

=> m^ed ≡ m (mod n)

又因為：

d x e ≡ 1 (mod f(n))

所以：

d x e = h f(n) + 1

代入原式，可以得到：

m^ed = m^{h f(n) + 1} ≡ m (mod n)

接下來分成兩種情況：



第一種： m 與 n 互質，則根據歐拉定理：

m^f(n) ≡ 1 (mod n)

所以原式成為：

m^{h f(n) + 1} = [(m^f(n))^h] x m = 1 x m = m ≡ m (mod n)

=> 則原式成立。



第二種： m 與 n 不互質

因為 n = p x q，且 p, q 為質數，所以 m 一定為 k x p 或 k x q。

以 m = kp 為例，又因為 q 是質數，且 m < n = p x q，所以 k 與 q 一定是互質，則根據歐拉定理：

(kp)^q-1 ≡ 1 (mod q)

所以下式也會成立：

[(kp)^q-1]^h(p-1) x kp ≡ kp (mod q)

=> (kp)^{(q-1) x (h(p-1))} x kp ≡ kp (mod q)

又因為：

d x e = h f(n) + 1

所以：

(kp)^{(q-1) x (h(p-1))} x kp = (kp)^{h(q-1)(p-1)+1} = (kp)^ed ≡ kp (mod q)

把 kp (mod q) 展開，可以寫成：

(kp)^ed = tq + kp

又因為 (kp)^ed 一定是 p 的位數，所以 (tq + kp) 也一定是 p 的倍數，所以 tq 一定也是 p 的倍數，又 p 與 q 互值，所以 t 一定是 p 的位數，所以：

(kp)^ed = tq + kp = t'pq + kp

又因為 m = kp 且 n = pq，代入上式後，得到：

m^ed = t'n + m ≡ m (mod n)

=> 原式成立。





RSA 的加密與解密範例



公鑰： e, n

私鑰： d, n

訊息： m

密文： c



取 p = 3、q = 11，所以 n = 33。

f(n) = (3-1)(11-1) = 20。

又條件為：

ed ≡ 1 (mod 20)

ed = 20k + 1，取 k = 1，令 e = 3、d = 7。

所以公鑰為： (3, 33)，私鑰為： (7, 33)。



假設訊息為 m = 17

加密： (17)³ (mod 33) = 29



密文 c = 29

解密： (29)⁷ (mod 33) = 17





Reference



輕鬆學習RSA加密演算法原理



RSA算法原理（二）

table td, table th {padding: 6px; border:1px solid #000000;}

table td, table th {padding: 6px; border:1px solid #000000;}

table td, table th {padding: 6px; border:1px solid #000000;}
如何取得圓所包含的像素點位置
在圖中已知一點 (x, y) 為圓的中心點，圓的半徑為 r，求該圓內的所有像素點位置？
 

table td, table th {padding: 6px; border:1px solid #000000;}
如何使挑選到的特徵點廣泛分佈於影像
Q: 在一張特徵點分佈不平均的圖片中，如何限制所挑選的特徵點能儘量分佈於整個圖片？
A:

利用廣度優先，將圖片分割成數個等大小區塊。

如果區塊個數少於要挑選的特徵點個數，則將特徵點個數多於一個的區塊再分割成數個等大小區塊，持續重複此步驟，直到區塊個數多於要挑選的特徵點個數。

最後每個區塊只取該區塊內強度最強的特徵點作代表，最有的區塊分割可能如下：

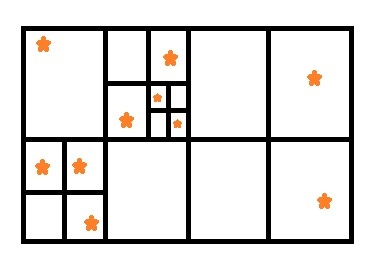
程式範例：(截取於 ORB-SLAM2 ORBextractor::DistributeOctTree())
while(lit != lNodes.end())
{
if(lit->bNoMore) // 如果只有一個特徵點，便不再分割
{
// If node only contains one point do not subdivide and continue
lit++;
continue;
}
else // 否則再細分為四個子區塊
{
// If more than one point, subdivide
ExtractorNode n1,n2,n3,n4;
lit->DivideNode(n1, n2, n3, n4);
// Add childs if they contain points
if(n1.vKeys.size() > 0)
{
lNodes.push_front(n1);
if(n1.vKeys.size() > 1)
{
nToExpand++;
vSizeAndPointerToNode.push_back(make_pair(n1.vKeys.size(),&lNodes.front()));
lNodes.front().lit = lNodes.begin();
}
}
if(n2.vKeys.size() > 0)
{
lNodes.push_front(n2);
if(n2.vKeys.size() > 1)
{
nToExpand++;
vSizeAndPointerToNode.push_back(make_pair(n2.vKeys.size(),&lNodes.front()));
lNodes.front().lit = lNodes.begin();
}
}
if(n3.vKeys.size() > 0)
{
lNodes.push_front(n3);
if(n3.vKeys.size() > 1)
{
nToExpand++;
vSizeAndPointerToNode.push_back(make_pair(n3.vKeys.size(),&lNodes.front()));
lNodes.front().lit = lNodes.begin();
}
}
if(n4.vKeys.size() > 0)
{
lNodes.push_front(n4);
if(n4.vKeys.size() > 1)
{
nToExpand++;
vSizeAndPointerToNode.push_back(make_pair(n4.vKeys.size(),&lNodes.front()));
lNodes.front().lit = lNodes.begin();
}
}
lit = lNodes.erase(lit);
continue;
}
}
Reference

文字內容 或 影像內容 部份參考、引用自網路，如有侵權，請告知，謝謝。