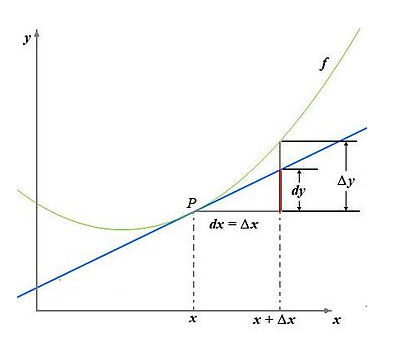
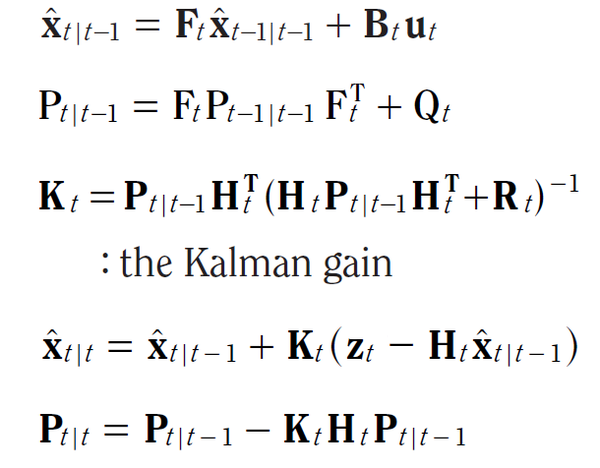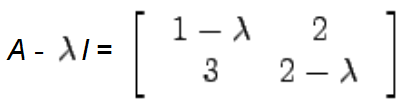 微分法則 (Differentiation rules)
微分法則 (Differentiation rules)silverwind1982 發表在 痞客邦 留言(0) 人氣(3,951)
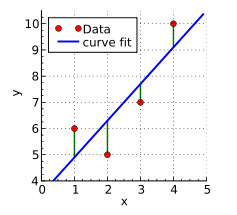
table td, table th {padding: 6px; border:1px solid #000000;}
silverwind1982 發表在 痞客邦 留言(0) 人氣(40,406)
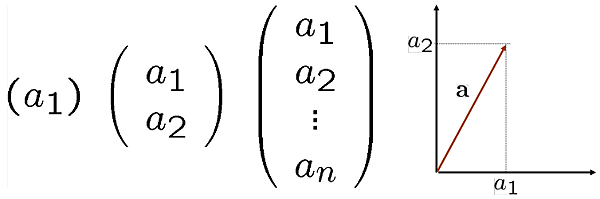
table td, table th {padding: 6px; border:1px solid #000000;}
silverwind1982 發表在 痞客邦 留言(0) 人氣(24,704)
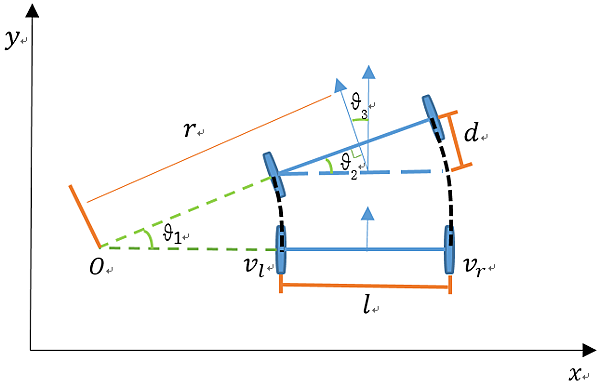
table td, table th {padding: 6px; border:1px solid #000000;}
silverwind1982 發表在 痞客邦 留言(0) 人氣(2,584)

table td, table th {padding: 6px; border:1px solid #000000;}
卡爾曼濾波器又稱為最佳線性濾波器(輸出值為輸入值的線性組合),為實現簡單、純時間域的濾波器,在實現過程中,所有關於不確定性的關係(雜訊),都會用到共變異數矩陣。
卡爾曼濾波器的五個基本公式:
X(k|k-1) = F X(k-1|k-1) + B U(k) ...(1)P(k|k-1) = F P(k-1|k-1) FT + Q ...(2)X(k|k) = X(k|k-1) + Kg(k) (Z(k) - H X(k|k-1)) ...(3)Kg(k) = P(k|k-1) HT / (H P(k|k-1) HT + R) ...(4)P(k|k) = (I - Kg(k) H) P(k|k-1) ...(5)簡單翻成白話分別為:
利用 k-1 的狀態,加上變化量,預估出 k 狀態。 ...(1)
利用 k-1 狀態的雜訊,配合步驟(1)預估 k 狀態的雜訊,預估出 k 狀態的雜訊。 ...(2)
利用預估出的 k 狀態 與 k 的測量狀態 搭配權重值(Kalman Gain) 完成更新 k 狀態。 ...(3)
權重值(Kalman Gain) 是由步驟(2)中的 k 狀態的雜訊 與 測量雜訊 經計算而求得。 ...(4)
最後利用 權重值(Kalman Gain) 更新 k 狀態的雜訊。 ...(5)
搭配圖示如下:
理解卡爾曼濾波器卡爾曼濾波器的主要步驟有兩個:預估 以及 測量更新,以下舉一個例子作簡單說明。
假設要利用卡爾曼濾波器來計算房間內每分鐘的溫度變化:
silverwind1982 發表在 痞客邦 留言(4) 人氣(61,882)

table td, table th {padding: 6px; border:1px solid #000000;}
silverwind1982 發表在 痞客邦 留言(0) 人氣(7,435)
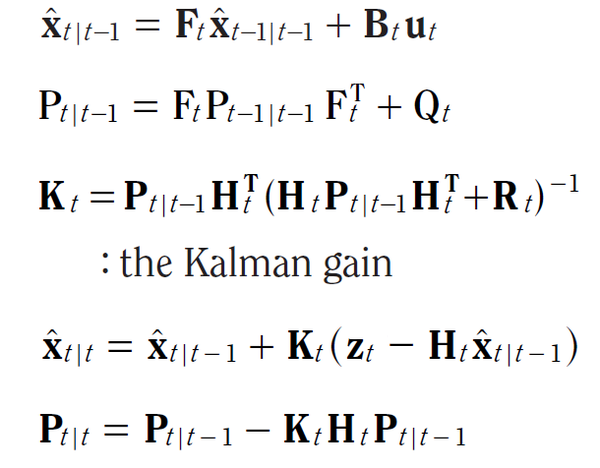
table td, table th {padding: 6px; border:1px solid #000000;}
silverwind1982 發表在 痞客邦 留言(0) 人氣(3,015)
table td, table th {padding: 6px; border:1px solid #000000;}
silverwind1982 發表在 痞客邦 留言(0) 人氣(18,122)
table td, table th {padding: 6px; border:1px solid #000000;}
silverwind1982 發表在 痞客邦 留言(0) 人氣(4,344)
table td, table th {padding: 6px; border:1px solid #000000;}
silverwind1982 發表在 痞客邦 留言(2) 人氣(317,948)