拾人牙慧

卡爾曼濾波器又稱為最佳線性濾波器(輸出值為輸入值的線性組合)，為實現簡單、純時間域的濾波器，在實現過程中，所有關於不確定性的關係(雜訊)，都會用到共變異數矩陣。

卡爾曼濾波器的五個基本公式：
X(k|k-1) = F X(k-1|k-1) + B U(k) ...(1)
P(k|k-1) = F P(k-1|k-1) F^T + Q ...(2)
X(k|k) = X(k|k-1) + Kg(k) (Z(k) - H X(k|k-1)) ...(3)
Kg(k) = P(k|k-1) H^T / (H P(k|k-1) H^T + R) ...(4)
P(k|k) = (I - Kg(k) H) P(k|k-1) ...(5)

簡單翻成白話分別為：
利用 k-1 的狀態，加上變化量，預估出 k 狀態。 ...(1)
利用 k-1 狀態的雜訊，配合步驟(1)預估 k 狀態的雜訊，預估出 k 狀態的雜訊。 ...(2)
利用預估出的 k 狀態 與 k 的測量狀態 搭配權重值(Kalman Gain) 完成更新 k 狀態。 ...(3)
權重值(Kalman Gain) 是由步驟(2)中的 k 狀態的雜訊 與 測量雜訊 經計算而求得。 ...(4)
最後利用 權重值(Kalman Gain) 更新 k 狀態的雜訊。 ...(5)

搭配圖示如下：





理解卡爾曼濾波器

卡爾曼濾波器的主要步驟有兩個：預估 以及 測量更新，以下舉一個例子作簡單說明。

假設要利用卡爾曼濾波器來計算房間內每分鐘的溫度變化：

• 預估：以經驗判斷，房間內的溫度是恆溫的，也就是下一分鐘的溫度會等於目前這分鐘的溫度。
  
  但事實上，房間未必是恆溫的，而且以經驗判斷出的溫度也可能包含誤差，這些誤差就是所謂的高斯白雜訊，也就是說，這些誤差與前後時間無關，並且符合高斯分配。


• 測量更新：在房間中，也利用溫度計來作溫度測量，而溫度計的測量值同樣也和實際值存在著誤差，這些誤差也是高斯白雜訊。

於是在某一分鐘內，會有兩個關於該房間溫度的值：

1. 根據經驗的預估值 (預估值)
2. 溫度計的值 (測量值)

接著利用這兩個值結合各自的雜訊來估算出房間的實際溫度值。

計算過程：

假設 經驗法則預估的誤差 與 溫度計的誤差 為已知的系統參數。

Step 1, state and covariance prediction
假設要預估 K 時刻的溫度，首先根據 K-1 時刻所推算的溫度來作預估。
假設 K-1 時刻所推算的房間溫度為 23度，則預估 K 時刻的房間溫度也是 23度。

又假設在 K-1 時刻所推算的房間溫度其(變異數)誤差值為 3，經驗法則預估值的(變異數)誤差為 4，則由 K-1 時刻的房間溫度及經驗法則來預估 K 時刻的溫度，其變異數為將他們各自的(變異數)誤差相加，也就是 3 + 4 = 7。

接著假設溫度計在 K 時刻的測量值為 25度，同時該溫度計的(變異數)誤差為 4度。


Step 2, Kalman gain correction and state correction
目前為止，在 K 時刻的房間溫度，預估值為 23度，測量值為 25度，那最後的溫度該如何算出？這兩個值是否有哪一個值是比較值得相信的？

這時候就要先計算 Kalman gain (Kg)，Kalman gain 的值是由預估值的(變異數)誤差值與測量值的(變異數)誤差值所計算而得，其(變異數)誤差值分別為 7 與 4：
Kg = 7 / (7 + 4) = 7/11 = ~0.64

由 Kalman gain 的值，推算出 K 時刻的溫度為：
預估值 + Kalman gain * (測量值 - 預估值)
=> 23 + 0.64 * (25 - 23) = 24.28

這邊可以看出，因為預估值(23度)的(變異數)誤差為 7，而測量值(25度)的(變異數)誤差為 4，所以測量值比較值得相信，故推算出來的值會比較偏向測量值。


Step 3, covariance correction
當然所推算出來的值與實際的溫度值還是存在著(變異數)誤差，該(變異數)誤差值與預估值的(變異數)誤差值(7度)有關，計算方式為：
(1 - Kg) * 7 = (1 - 0.64) * 7 = 0.36 * 7 = 2.52
算出來的 2.52 度的(變異數)誤差值，對應到 K-1 時刻所推算的房間溫度誤差值 3 度。
也就是說在 K 時間，所推算出的房間溫度為 24.28 度，(變異數)誤差值為 2.52 度，接著可以再進行 K+1 時刻的房間溫度推算。

根據以上規則，卡爾曼濾波器可以一直迭代下去。

以下開始討論真正工程系統上所使用的卡爾曼濾波器。




卡爾曼濾波器演算法

首先，先介紹一個離散控制過程的系統，該系統可以用一個線性隨機微分方程式(Linear Stochastic equation)來表示：

X(k) = F X(k-1) + B U(k) + W(k)

該系統的測量值為：

Z(k) = H X(k) + V(k)

其中：

• X(k) 是 k 時刻的系統狀態
• U(k) 是 k 時刻對系統的控制量
• F 和 B 是系統參數，對於多模型系統，他們是矩陣
• Z(k) 是 k 時刻的測量值
• H 是測量系統的參數，對於多測量系統，H 是矩陣
• W(k) 與 V(k) 分別表示過程和測量的雜訊，被假設為高斯白雜訊，covariance 分是 Q 及 R，這裡假設他們不會隨系統狀態變化而變化

對於滿足上述條件(線性隨機微分系統，過程和測量的雜訊皆為高斯白雜訊)的系統來說，卡爾曼濾波器是最佳的資訊處理器，接著會結合他們的 covariance 來推算系統的最佳輸出值(類似上一節的溫度例子)。

首先，利用系統的過程模型，來預估下一狀態的系統，假設目前的系統狀態是 k，則根據系統的過程模型，可以基於系統的上一狀態來預估出目前的狀態：
X(k|k-1) = F X(k-1|k-1) + B U(k) ...(1)

式(1)中，X(k|k-1)是利用上一狀態預測的結果，X(k-1|k-1)是系統在上一狀態所推算的結果，U(k)是系統在目前狀態的控制量，如果沒有控制量，可以為 0。

目前為止，系統結果已經更新了，接著需要更新的是 X(k|k-1) 的 covariance，以 P 表示 covariance：
P(k|k-1) = F P(k-1|k-1) F^T + Q ...(2)

至於為何需要乘上兩邊，這是因為共變異數矩陣的性質：
cov(x, x) = cov(x, x)
cov(Ax, Bx) = A cov(x, x) B^T
=> cov(Ax, Ax) = A cov(x, x) A^T

式(2)中，P(k|k-1) 是 X(k|k-1) 對應的 covariance，P(k-1|k-1) 是 X(k-1|k-1) 對應的 covariance，F^T 表示 F 的轉置矩陣，Q 是系統過程的 covariance；式(1) 及 式(2) 就是卡爾曼濾波器5個公式當中的前兩個，也就是對系統狀態的預估。

現在有了狀態的預估結果，需要再取得目前狀態的測量值(Z(k))，接著結合預估值與測量值，就可以推算出目前狀態(k) 的最佳推算值 X(k|k)：
H X(k|k) = H X(k|k-1) + Kg'(k) (Z(k) - H X(k|k-1)) ...(A)
此時對應的 covariance 為：
H P(k|k) H^T = H P(k|k-1) H^T - Kg'(k) H P(k|k-1) H^T ...(B)

從之前的定義，可以知道 Z(k) 與 X(k) 之間的單位轉換矩陣為 H，而 Z(k) 的 covariance 為 R：
Z(k) = H X(k) + V(k)

此時 Kg'(k) 為權重比，是由 H X(k|k-1) 及 Z(k) 的 covariance 來決定，計算方式如下：
Kg'(k) = H P(k|k-1) H^T / (H P(k|k-1) H^T + R) ...(C)
H X(k|k-1) 的 covariance 為：H P(k|k-1) H^T。

接著簡化 公式 A，同時乘上 H^-1，進而推導出卡爾曼濾波器的第三個基本公式：
X(k|k) = X(k|k-1) + Kg(k) (Z(k) - H X(k|k-1)) ...(3)
其中 Kg 為 Kalman Gain，為 H^-1 * Kg'，由公式 C 可得：
Kg(k) = P(k|k-1) H^T / (H P(k|k-1) H^T + R) ...(4)

目前為止，已經計算出 k 狀態下的最佳推算值 X(k|k)，但是為了要讓卡爾曼濾波器可以不斷的運行下去，還需要更新 X(k|k) 的 covariance，簡化 公式 B 可以得到：
P(k|k) = P(k|k-1) - Kg(k) H P(k|k-1) =>
P(k|k) = (I - Kg(k) H) P(k|k-1) ...(5)

其中 I 為 1 的矩陣，對於單模型、單測量系統，I = 1；當系統進入 k+1 狀態時，P(k|k) 就會是 式(2) 的 P(k-1|k-1)，如此，演算法就可以一直遞迴下去。

卡爾曼濾波器的基本原理如上所述，式(1) ~ 式(5) 就是卡爾曼濾波器的五個基本公式，根據這五個公式，就可以在電腦上實作卡爾曼濾波器。

以下，舉實際運行的例子。




結合溫度計實例

卡爾曼濾波器的五個基本公式：
X(k|k-1) = F X(k-1|k-1) + B U(k) ...(1)
P(k|k-1) = F P(k-1|k-1) F^T + Q ...(2)
X(k|k) = X(k|k-1) + Kg(k) (Z(k) - H X(k|k-1)) ...(3)
Kg(k) = P(k|k-1) H^T / (H P(k|k-1) H^T + R) ...(4)
P(k|k) = (I - Kg(k) H) P(k|k-1) ...(5)

根據上述所提到對房間進行溫度推算的例子中，把房間看成是一個系統，然後對這個系統建立模型，當然模型不需要非常準確，因此可以假設預估該房間的溫度與前一時刻的溫度是相同的，所以 F = 1，沒有控制量，所以 U(k) = 0，因此：
X(k|k-1) = X(k-1|k-1) ...(6)

又因為 F = 1，所以 式(2) 可以改寫為：
P(k|k-1) = P(k-1|k-1) + Q ...(7)

也因為測量值是由溫度計取得，與溫度直接對應，所以 H = 1，式(3) ~ 式(5) 可以改寫為：
X(k|k) = X(k|k-1) + Kg(k) (Z(k) - X(k|k-1)) ...(8)
Kg(k) = P(k|k-1) / (P(k|k-1) + R) ...(9)
P(k|k) = (1 - Kg(k)) P(k|k-1) ...(10)




在 OpenCV 的實作程式碼為：

std::srand(std::time(0));

double Z[100] = {0};
for (int i = 0; i < 100; ++i) {
Z[i] = 19 + (std::rand() % 201) / 100.0; // 測量值 + 模擬雜訊: 19 ~ 21
}

double X = 0; // 狀態推算值
double P = 3; // 狀態推算值的共變異數
double F = 1; // 狀態轉換
double Q = 4; // 狀態預估模型的共變異數
double H = 1; // 測量值
double R = 4; // 測量值的共變異數矩陣
double I = 1;
double K = 0; // Kalman Gain

for (int i = 0; i < 100; ++i) {
X = X; // 預估值
P = P + Q; // 預估值雜訊
K = P / (P + R); // Kalman Gain
X = X + K * (Z[i] - X); // 推算值
P = (I - K) * P; // 推算值雜訊
}



結合小汽車實例

以小汽車來舉例，其參數如下：

狀態 x_t 為 位置 與 速度：


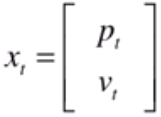
控制量 u_t 為 加速度，可以用來計算 x_t：


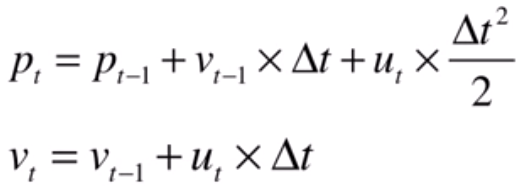
從上述公式可以看到輸出值為輸入值的線性組合，改寫為矩陣型式如下：


再簡化公式為：
x_t^- = F_tx_t-1 + B_tu_t ...(11)

F 為狀態轉移矩陣，表示如何從上一時刻的推算狀態預估出目前時刻的狀態
B 為控制矩陣，表示控制量 u 如何作用於目前時刻的狀態

在本例中，以共變異數矩陣 P 來表示該時刻的推算狀態的不確定性 - 也就是雜訊。
而狀態轉換矩陣 F 可以用來將不確定性傳遞到下一個時刻：
P_t^- = F P_t-1 F^T

除了將上一時刻的不確定性作傳遞之外，由於預測模型也會有不確定性(Q)，所以在各個時刻其不確定性的傳遞關係須要修正為：
P_t^- = F P_t-1 F^T + Q ...(12)

假設利用紅外線測距儀來測量小汽車在每個時刻的位置(Z_t)，可以得到：
Z_t = H x_t + v

其中：
H 為 測量值矩陣， H = [1 0]
v 為 測量值的雜訊

另外測量值雜訊的共變異數矩陣以 R 表示。

有了測量值後，就可以對狀態值進行更新：
x_t = x_t^- + K_t (z_t - Hx_t^-) ...(13)

其中 K_t 為卡爾曼系數，公式為：
K_t = P_t H^T (HP_t^-H^T + R)^-1 ...(14)

卡爾曼系數的主要作用有兩個：

• 權衡預估值共變異數矩陣(P) 與 測量值共變異數矩陣(R) 兩個值之間的大小，來決定要比較相信 預測模型 還是 測量模型。
• 將 測量值 的型式轉換為 預測值狀態 的型式，如此才能對預測值作修正。

最後一個步驟為更新推算狀態的雜訊分佈，供下一次迭代使用：
P_t = (I - K_tH) P^-1 ...(15)

在 matlab 的實作程式碼為：

Z = (1:100); % 測量值
noise = randn(1, 100); % 模擬測量值的雜訊
Z = Z + noise; % 測量值+雜訊

X = [0; 0]; % 狀態推算值
P = [1 0; 0 1]; % 狀態推算值的共變異數矩陣
F = [1 1; 0 1]; % 狀態轉換矩陣
Q = [0.0000001 0; 0 0.0000001]; % 狀態預估模型的共變異數矩陣
H = [1 0]; % 測量值矩陣
R = 1; % 測量值的共變異數(矩陣)

figure;
hold on;

for i = 1:100
X_ = F * X; % kalman filter eq. (1)，缺少控制量 U
P_ = F * P * F' + Q; % kalman filter eq. (2)
K = P_ * H' / (H * P_ * H' + R); % kalman filter eq. (3)
X = X_ + K * (Z(i) - H * X); % kalman filter eq. (4)
P = (eye(2) - K * H) * P_; % kalman filter eq. (5)

plot(X(1), X(2));
end



在 OpenCV 的實作程式碼為：

std::srand(std::time(0));

float Z[100] = {0};
for (int i = 0; i < 100; ++i) {
Z[i] = i + (std::rand() % 100) / 100.0; // 測量值 + 模擬雜訊
}

cv::Mat X = (cv::Mat_<float>(2,1) << 0, 0); // 狀態推算值
cv::Mat P = (cv::Mat_<float>(2,2) << 1, 0, 0, 1); // 狀態推算值的共變異數矩陣
cv::Mat F = (cv::Mat_<float>(2,2) << 1, 1, 0, 1); // 狀態轉換矩陣
cv::Mat Q = (cv::Mat_<float>(2,2) << 0.0000001, 0, 0, 0.0000001); // 狀態預估模型的共變異數矩陣
cv::Mat H = (cv::Mat_<float>(1,2) << 1, 0); // 測量值矩陣
cv::Mat R = (cv::Mat_<float>(1,1) << 1); // 測量值的共變異數矩陣
cv::Mat I = (cv::Mat_<float>(2,2) << 1, 0, 0, 1);
cv::Mat K = (cv::Mat_<float>(2,1) << 0, 0);

for (int i = 0; i < 100; ++i) {
X = F * X; // 預估值
P = F * P * F.t() + Q; // 預估值雜訊
K = P * H.t() / ((cv::Mat)(H * P * H.t() + R)).at<float>(0,0); // Kalman Gain
X = X + K * (Z[i] - H * X); // 推算值
P = (I - K * H) * P; // 推算值雜訊
}



數學補充

共變異數(Covariance) 在機率論和統計學中用於衡量兩個變量的總體誤差。
期望值(平均數)分別為 E(X) = μ 與 E(Y) = v 的兩個實數隨機變量 X 與 Y 之間的共變異數定義為：
cov(X,Y) = E((X - μ) (Y - v)) = E(XY) - μv

在統計學與機率論中，共變異數矩陣（也稱離差矩陣、變異數-共變異數矩陣）是一個矩陣，其 i, j 位置的元素是第 i 個與第 j 個隨機向量（即隨機變量構成的向量）之間的共變異數。

變異數(Variance) 是共變異數的一種特殊情況，即當兩個變量是相同的情況，定義為：
Var(x) = E[(X - μ)²]
又因為 μ = E[X]，可以展開成為：
Var(x) = E[X² - 2XE[x] + (E[X])²] = E[X²] - 2E[X]E[X] + (E[X])² = E[X²] - (E[X])²
上述的表示式可以計為：平方值的平均減去平均的平方

標準差(Standard Deviation, SD) 是一組數值自平均值分散開來的程度的一種測量觀念，數學符號σ，定義為變異數的算術平方根，反映組內個體間的離散程度；標準差與期望值之比為標準離差率。




Kalman Filter 相關文章

Understanding the Basis of the Kalman Filter Via a Simple and Intuitive Derivation

卡爾曼濾波 (Kalman Filter)




Reference

卡爾曼濾波器(Kalman Filter) 說明與介紹
卡爾曼濾波器的原理以及在 matlab 中的實現
Kalman Filter with MATLAB CODE
How a Kalman filter works, in pictures
The Extended Kalman Filter: An Interactive Tutorial for Non-Experts

文字內容 或 影像內容 部份參考、引用自網路，如有侵權，請告知，謝謝。