一、廣義角三角函數:
sin(θ) 與 cos(θ) 的定義:
在坐標平面上,以原點 O 為圓心,有一個半徑等於 r 的圓,給定一個廣義角 θ,規定 θ 的起始邊為 x 軸的正方向,θ 角的頂點為原點,依逆時針旋轉,則根據 θ 的旋轉量,可決定終邊的位置。
假設終邊這條射線與圓交於P(x,y),則定義:
sin(θ) = y / r
cos(θ) = x / r
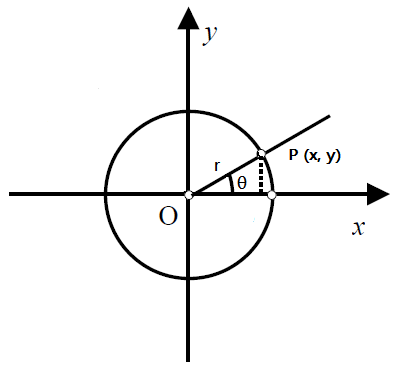
其它三角函數的定義:
tan(θ) = sin(θ) / cos(θ) = y / x
cot(θ) = cos(θ) / sin(θ) = x / y
sec(θ) = 1 / cos(θ) = r / x
csc(θ) = 1 / sin(θ) = r / y
三角函數的關係:
平方關係:
sin2(θ) + cos2(θ) = 1
商數關係:
tan(θ) = sin(θ) / cos(θ) ;
cot(θ) = cos(θ) / sin(θ)
餘角關係:
sin(90°-θ) = cos(θ) ; cos(90°-θ) = sin(θ) ;
tan(90°-θ) = cot(θ) ; cot(90°-θ) = tan(θ) ;
sec(90°-θ) = csc(θ) ; csc(90°-θ) = sec(θ)
三角函數的化簡:
化簡到 360° 內:
sin(n*360°+θ) = sin(θ)
cos(n*360°+θ) = cos(θ)
tan(n*360°+θ) = tan(θ)
化簡到 180° 內:
sin(180°+θ) = -sin(θ);
sin(180°-θ) = sin(θ);
cos(180°+θ) = -cos(θ);
cos(180°-θ) = -cos(θ);
tan(180°+θ) = tan(θ);
tan(180°-θ) = -tan(θ)
餘角關係
sin(90°+θ) = cos(θ);
cos(90°+θ) = -sin(θ);
tan(90°+θ) = -cot(θ);
sin(270°-θ) = -cos(θ);
cos(270°-θ) = -sin(θ);
tan(270°-θ) = cot(θ)
負角關係:
sin(-θ) = -sin(θ);
cos(-θ) = cos(θ);
tan(-θ) = -tan(θ)
二、三角函數在平面幾何上的應用:
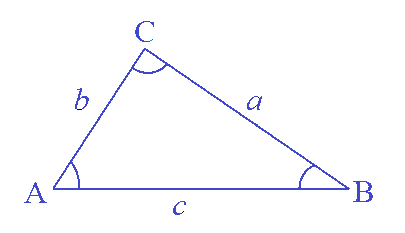
正弦定理:(Sine Rule)
在 ∆ABC 中,以 a, b, c 分別為 ∠A, ∠B, ∠C 的對邊長,則:
a / sin(A) = b / sin(B) = c / sin(C) = 2R
其中 R 為 ∆ABC 的外接圓半徑。
餘弦定理:(Cosine Rule)
在 ∆ABC 中,以 a, b, c 分別為 ∠A, ∠B, ∠C 的對邊長,則:
a2 = b2 + c2 - 2bc * cos(A)
b2 = a2 + c2 - 2ac * cos(B)
c2 = a2 + b2 - 2ab * cos(C)
三、三角函數的公式:
複角公式:(合、分角公式) (Angle-Sum and -Difference Identities)
sin(α + β) = sin(α)cos(β) + cos(α)sin(β)
sin(α – β) = sin(α)cos(β) – cos(α)sin(β)
cos(α + β) = cos(α)cos(β) – sin(α)sin(β)
cos(α – β) = cos(α)cos(β) + sin(α)sin(β)
tan(a + b) = [tan(a) + tan(b)] / [1 - tan(a)tan(b)]
tan(a - b) = [tan(a) - tan(b)] / [1 + tan(a)tan(b)]
倍角公式:(Double-Angle Identities)
sin(2x) = 2sin(x)cos(x)
cos(2x) = cos2(x) – sin2(x)
= 1 – 2sin2(x)
= 2cos2(x) – 1
tan(2x) = [2 tan(x)] / [1 - tan2(x)]
半角公式:(Half-Angle Identities)
sin(x/2) = +/- sqrt[(1 - cos(x))/2]
cos(x/2) = +/- sqrt[(1 + cos(x))/2]
tan(x/2) = +/- sqrt[(1 - cos(x))/(1 + cos(x))]
= (1 - cos(x)) / sin(x)
= sin(x) / (1 + cos(x))
和差化積:(Sum Identities)
sin(x) + sin(y) = 2 sin[(x+y)/2] cos[(x-y)/2]
sin(x) - sin(y) = 2 cos[(x+y)/2] sin[(x-y)/2]
cos(x) + cos(y) = 2 cos[(x+y)/2] cos[(x-y)/2]
cos(x) - cos(y) = -2 sin[(x+y)/2] sin[(x-y)/2]
積化和差:(Product Identities)
sin(x) cos(y) = (1/2) [sin(x+y) + sin(x-y)]
cos(x) sin(y) = (1/2) [sin(x+y) - sin(x-y)]
cos(x) cos(y) = (1/2) [cos(x-y) + cos(x+y)]
sin(x) sin(y) = (1/2) [cos(x-y) - cos(x+y)]
背誦口訣:sine cosine cosine sine, cosine cosine sine sine
把這個口訣唸得愈順愈好,這是公式中 sin 跟 cos 的順序,接著再配合自己的理解來背。
全站熱搜


 留言列表
留言列表
