雙輪機器人的移動軌跡
利用已知的左、右兩輪的速度(vl, vr)及相隔距離(l),推導出雙輪機器人的移動速度(v)、偏移角度(θ)、旋轉半徑(r)、角加速度(w)。
它們彼此間的關係為:
v = (vr + vl) / 2
w = (vr - vl) / l (unit: radian/time)
r = v / w = (l * (vr + vl)) / (2 * (vr - vl))
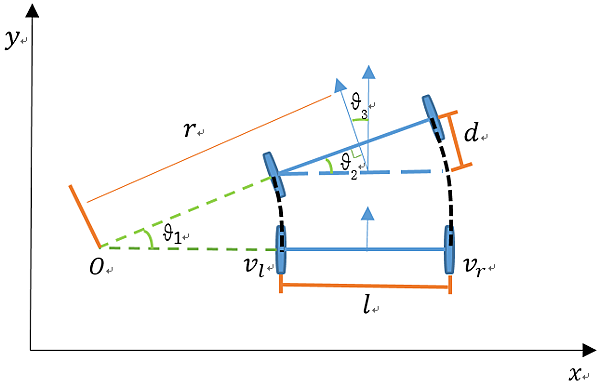
機器人可能的移動軌跡如上圖,其中:
一開始先計算機器人的偏移角度,也就是 θ3,由上圖,根據相似三角形原理,可以得到:
θ1 = θ2 = θ3
也就是說機器人的偏移角度,會跟它繞著運動軌跡圓心所旋轉的角度相等。
又因為當角度很小時,θ 會近似於 sin(θ) 近似於 tan(θ) (參考網站),因此可以得到:
θ2 近似於 sin(θ2) 近似於 (d / l) = ((vr - vl) * △t) / l
所以機器人的角速度(w) 為:
θ3 / △t = (vr - vl) / l
根據圓周長公式:
圓周長 = 圓半徑 x 圓弧度 => 圓半徑 = 圓周長 / 圓弧度
又因為單位時間內圓周長的值為 速度 * △t,圓弧度的值為 角速度 * △t
因為可以得推導出:
圓半徑 = (速度 * △t) / (角速度 * △t) = 速度 / 角速度
=> r = v / w
因此有了機器人的速度、角速度後,可以推算出機器人圓弧運動的半徑(r):
r = v / w = (l * (vr + vl)) / (2 * (vr - vl))
從上述公式可以發現,如果左、右兩輪的速度幾乎相等,則半徑為無限大,也就是機器人的運動方向為直線。
最後綜合左、右輪速度及左、右輪距離的公式,與機器人的速度、角速度及旋轉半徑的關係如下:
v = (vr + vl) / 2
w = (vr - vl) / l (unit: radian/time)
r = v / w = (l * (vr + vl)) / (2 * (vr - vl))
Reference
航迹推演(Odometry)
[數學] 困惑高中生的近似值
文字內容 或 影像內容 部份參考、引用自網路,如有侵權,請告知,謝謝。
利用已知的左、右兩輪的速度(vl, vr)及相隔距離(l),推導出雙輪機器人的移動速度(v)、偏移角度(θ)、旋轉半徑(r)、角加速度(w)。
它們彼此間的關係為:
v = (vr + vl) / 2
w = (vr - vl) / l (unit: radian/time)
r = v / w = (l * (vr + vl)) / (2 * (vr - vl))

機器人可能的移動軌跡如上圖,其中:
- vl、vr 分別是左、右兩輪的速度,已知。
- l 為兩輪子的相隔距離,已知。
- θ3 為機器人的偏移(旋轉)角度,未知。
- r 為旋轉半徑,未知。
- d 為左、右兩輪移動距離的差距,公式為: (vr - vl) * △t。
- v 為機器人的移動速度,為左、右輪速度的平均,公式為: (vl + vr) / 2。
一開始先計算機器人的偏移角度,也就是 θ3,由上圖,根據相似三角形原理,可以得到:
θ1 = θ2 = θ3
也就是說機器人的偏移角度,會跟它繞著運動軌跡圓心所旋轉的角度相等。
又因為當角度很小時,θ 會近似於 sin(θ) 近似於 tan(θ) (參考網站),因此可以得到:
θ2 近似於 sin(θ2) 近似於 (d / l) = ((vr - vl) * △t) / l
所以機器人的角速度(w) 為:
θ3 / △t = (vr - vl) / l
根據圓周長公式:
圓周長 = 圓半徑 x 圓弧度 => 圓半徑 = 圓周長 / 圓弧度
又因為單位時間內圓周長的值為 速度 * △t,圓弧度的值為 角速度 * △t
因為可以得推導出:
圓半徑 = (速度 * △t) / (角速度 * △t) = 速度 / 角速度
=> r = v / w
因此有了機器人的速度、角速度後,可以推算出機器人圓弧運動的半徑(r):
r = v / w = (l * (vr + vl)) / (2 * (vr - vl))
從上述公式可以發現,如果左、右兩輪的速度幾乎相等,則半徑為無限大,也就是機器人的運動方向為直線。
最後綜合左、右輪速度及左、右輪距離的公式,與機器人的速度、角速度及旋轉半徑的關係如下:
v = (vr + vl) / 2
w = (vr - vl) / l (unit: radian/time)
r = v / w = (l * (vr + vl)) / (2 * (vr - vl))
Reference
航迹推演(Odometry)
[數學] 困惑高中生的近似值
文字內容 或 影像內容 部份參考、引用自網路,如有侵權,請告知,謝謝。
全站熱搜


 留言列表
留言列表
