如何取得圓所包含的像素點位置－拾人牙慧

如何取得圓所包含的像素點位置

在圖中已知一點 (x, y) 為圓的中心點，圓的半徑為 r，求該圓內的所有像素點位置？

算法一，直接使用畢氏定理

根據畢氏定理，該圓中 y 軸位置在 x 軸為 (y + n) 的像素個數為：
squrt(r² - n²)，其中 n = 0 ~ r。

因此給定一個任意點 (a, b)，其像素點的 x 軸的範圍為：
a-r, a-r+1, a-r+2, ..., a, a+1, a+2, ..., a+r

在每個 x 軸的像素中，其 y 軸的像素點範圍即為 squrt(r² - n²)，其中 n = -r ~ r，依 x 軸的位置而定。

以 C 語言來表示：

int i, count;
double radius = (double) atoi(argv[1]);
double radius_square = radius * radius;
int array1[9000] = {'\0'};

for (i = 0; i <= radius; ++i) {
    count = sqrt(radius_square - (i * i));
    array1[i] = count;
}

算法二，使用畢氏定理，且考慮圓的對稱性

考量到圓具有對稱性的特點，而為了滿足對稱性，必須先計算其對稱點，假設圓的中心點為 (x, y)，半徑為 r，則右上四分之一圓的對稱點為 (x + r / sqrt(2), y + r / sqrt(2))。

或者是說，為了減少計算量，而利用圓的對稱性，來計算出接下來的像素點個數。

一開始，同樣也是利用畢氏定理，該圓中 y 軸位置在 (y + n) 的像素個數為：
squrt(r² - n²)，其中 n: 1 ~ r / sqrt(2)。

為了保証滿足對稱性，或是說利用對稱性， x 軸位置在大於對稱點的 x 值，也就是 x + r / sqrt(2) 後，其所包含的像素點個數是以上一步驟的計算結果為基礎，再進行推算而得。

其中 r / sqrt(2) 的除法，為了方便計算可以換算為 r * sqrt(2) / 2。

圖形表示為：

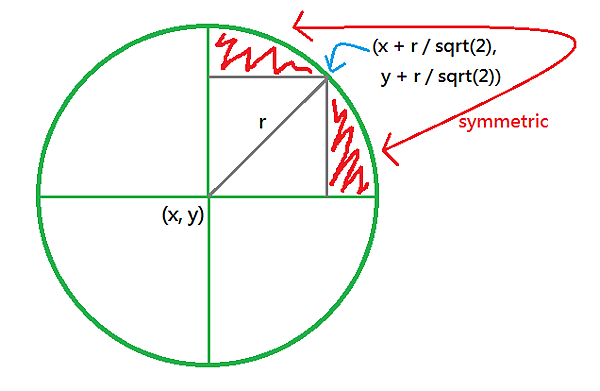
以 C 語言來表示：

    int i, i0, count;
    double radius = 5;
    double radius_square;
    double symmetric_x;
    int symmetric_x_max, symmetric_x_min;
    int array1[9000] = {'\0'};
    int array2[9000] = {'\0'};

    radius = (double) atoi(argv[1]);
    radius_square = radius * radius;

    // 計算對稱點
    symmetric_x = (radius * sqrt(2) / 2);
    symmetric_x_max = (int) (symmetric_x + 1);
    if (symmetric_x - (int) symmetric_x > 0) {
        symmetric_x_min = (int) (symmetric_x + 1);
    }
    printf("symmetric_x = %f vs. %d vs. %d\n", symmetric_x, symmetric_x_max, symmetric_x_min);

    for (i = 0; i <= (int)symmetric_x; ++i) {
        count = sqrt(radius_square - (i * i));
        array2[i] = count;
    }

    // 確保圓的對稱性，利用對稱性來計算
    for (i = radius, i0 = 0; i >= (int)symmetric_x; --i) {
        while (array2[i0] == array2[i0 + 1]) {
            ++i0;
        }
        array2[i] = i0;
        ++i0;
    }

程式範例：(截取於 ORB-SLAM2 ORBextractor::ORBextractor())

umax.resize(HALF_PATCH_SIZE + 1); // HALF_PATCH_SIZE 為圓的半徑

int v, v0, vmax = cvFloor(HALF_PATCH_SIZE * sqrt(2.f) / 2 + 1); // 計算對稱點
int vmin = cvCeil(HALF_PATCH_SIZE * sqrt(2.f) / 2);

const double hp2 = HALF_PATCH_SIZE*HALF_PATCH_SIZE;
for (v = 0; v <= vmax; ++v) {
    umax[v] = cvRound(sqrt(hp2 - v * v)); // 利用畢氏定理計算像素數目
}

// Make sure we are symmetric
for (v = HALF_PATCH_SIZE, v0 = 0; v >= vmin; --v) // 確保圓的對稱性
{
    // 利用 umax[] 數列的差值，來推出
    while (umax[v0] == umax[v0 + 1])
        ++v0;
    umax[v] = v0;
    ++v0;
}

一開始研究這段程式碼時，還以為如果直接用畢氏定理推算像素點的個數會導致對稱性不滿足，但經過實作比較後，發現對稱性還是存在的，尚未發現有哪個半徑的值經計算後，不滿足對稱性的。

如此，難道用對稱性來計算的方式是為了減少計算的時間？