這是一篇翻譯文,原文為:
A Guide To using IMU (Accelerometer and Gyroscope Devices) in Embedded Applications.
這篇文章是寫給所有對於 內部微機電系統 (inertial MEMS, Micro-Electro-Mechanical Systems) 感應器感興趣的人,特別是針對加速度計與陀螺儀以及這兩個感應器在 IMU 上如何搭配合作。

IMU 原件:Acc_Gyro_6DOF 在 MCU - UsbThumb 上,提供 USB/Serial 連線。
這篇文章包含基本而重要的觀念:
- 加速度計測量值的意義
- 陀螺儀測量值的意義
- 如何將這兩個感應器的輸出數值轉換為物理單位(在加速度計單位為 g;在陀螺儀單位為 deg/s)
- 如何結合加速度計與陀螺儀的測量值,以得到該裝置相對於地平面之間,較為準確的旋轉方位。
文章內容會試著以簡單的數學來說明,如果已經瞭解 Sine/Cosine/Tangent,則應該可以讀懂本篇文章並應用這些觀念在任何平台上,例如:Arduino, Propeller, Basic Stamp, Atmel chips, Microchip PIC ... 等等。可能有些人會覺得需要很複雜的數學才能學會如何使用 IMU ((complex FIR or IIR filters such as Kalman filters, Parks-McClellan filters, etc),這些主題有興趣的讀者可以好好研究,並取得極好但複雜的結果,只是作者個人習慣以基本的數學來解釋,並以簡單為原則,因為愈簡單的系統愈容易監視並控制,另一方面,許多嵌入式系統並沒有足夠的效能及資源來實作需要矩陣運算的複雜演算法。
這篇文章所使用的 IMU 為作者自行設計的 Acc_Gyro Accelerometer + Gyro IMU,本文中所使用的參數都是基於此裝置,這個裝置相當適合入門使用,它包含下列三部分:
- LIS331AL - 類比三軸 2G 加速度計
- LPR550AL - 雙軸(Pitch and Roll),500 deg/second 陀螺儀
- LY550ALH - 單軸(Yaw)陀螺儀(這個元件在本篇文章中沒有用到,主要是作用於 DCM Matrix implementation)
整體來看,這個擁有六個自由度的 IMU 是一個很實用的聯合裝置,下文會作詳細說明。
第一部分 加速度計
先從加速度計來看,當提到加速度計時,為了方便理解,可以想像為一顆球存在於一個立方體的盒子裡:
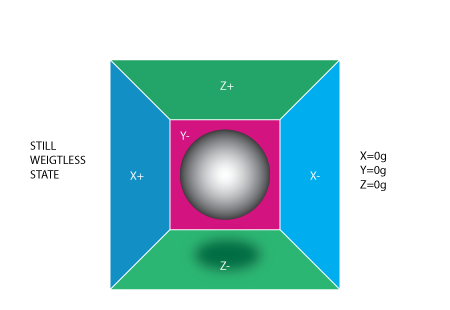
如果將這個盒子放置在一個沒有重力或沒有任何外力可以影響盒子內的球的地方,則這盒子內的球會飄浮在盒子的正中央,可以想像成把盒子帶到遠離各個星體的外太空,或是放在繞著地球轉的無重力太空船上,從上圖可以看到在 X, Y, Z 軸方向各有兩面牆(為了可以看到盒子的內部情況,移走 Y+ 的牆),想像每面牆都是可以偵測壓力的,如果突然將盒子往左邊移(加速度為 1g = 9.8 m/s2),則盒內的球會撞上牆 X-,如果測量球施加到牆上的壓力,則可以在 X 軸上得到 -1g 的數值。
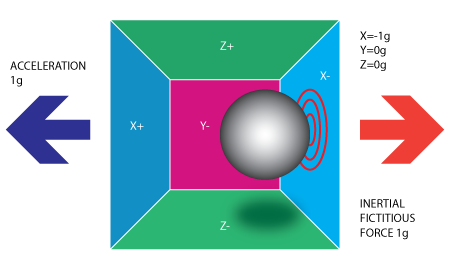
這邊要注意的是加速度計所偵測到的力的方向會與所施加的加速度方向相反,這樣的力稱為慣性力,從這個例子可以得知,加速度計是利用力施加到盒子的六個面(上例是牆,實際上可以是彈簧或其它東西),進而作間接測量,該力可以由加速度所造成,不過從下例中,可以看到會影響加速度計的並不是只有加速度。
如果將這個盒子放在地球上,則盒子內的球會在落在 Z- 的牆上,並施加 1g 的力,如下圖所示:
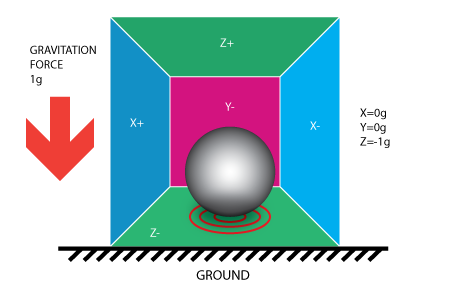
在這個例子中,盒子沒有被移動,但仍然可以在 Z 軸上測到 -1g 的加速度,球所施加在牆上的壓力是由重力所造成,理論上,它可以是任何種類的力,舉例來說,如果是鐵球的話,則會受磁鐵的磁力所影響,也就是說,加速度計在本質上所測量到的值並不是加速度,只是加速度所造成的慣性力,碰巧會被加速度計的偵測機制所測量到。
雖然微機電系統感應器的實際建構並不是以上述的模型來實作,但在解決加速度計相關的問題上,該模型是相當有幫助的;實際上,也是真的有相似的感應器在內部有一顆金屬球,稱為 tilt switch,但這種是比較原始的感應器,而且只能判斷在某個角度範圍內是否有傾斜,而不是傾斜的程度。
目前我們分析了加速度計在單一軸向的輸出值,這也是單軸加速度計所能得到的測量值;三軸加速度計的測量值則來自於該感應器可以在三個軸向偵測慣性力,回到盒子模型,如果將盒子順時針旋轉 45°,則盒裡的球會將力施加到 Z- 及 X- 兩面牆上,如下圖所示:
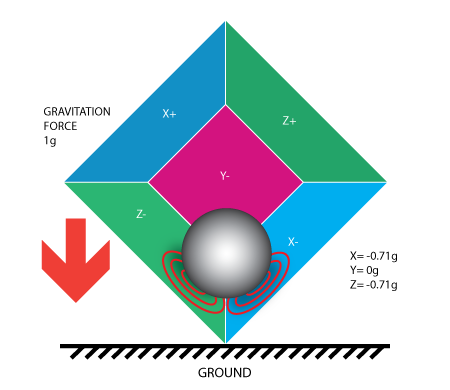
上圖中的值 0.71 g 並不是隨便給的,而是真實存在的值,約為 SQRT(1/2),原因再介紹完下個加速度計的模型後會更清楚。
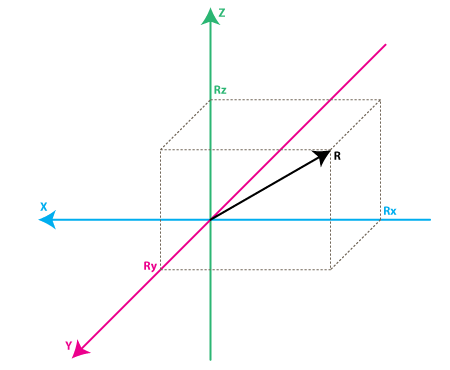
上圖的模型中,保留了三軸的顏色,可以方便與上一個模型作轉換,在這個模型中,三軸與上一個模型的六個面分別呈垂直狀態,圖中的向量 R,是加速度計所量測到的向量力(它可以是重力或是上例中的慣性力或是兩者同時存在),Rx, Ry, Rz 是向量 R 分別在 X, Y, Z 軸上的投影,他們的關系為:
R2 = Rx2 + Ry2 + Rz2 (Eq. 1)
這基本上也就是空間中的畢氏定理。
還記得剛剛提到的值 SQRT(1/2) ~ 0.71,如果將這個值帶入上述公式,重力加速度為 1g,則可以驗証:
12 = (-SQRT(1/2))2 + 02 + (-SQRT(1/2))2
將 Eq. 1 中以 R = 1, Rx = -SQRT(1/2), Ry = 0, Rz = -SQRT(1/2) 作取代。
經過一長串的推導後,所得結果愈來愈接近真實的加速度計,Rx, Ry, Rz 的值與現實生活中,加速度計所輸出用來作各式各樣計算的值為線性相關。
再往下繼續計算之前,先看看加速度計是如何傳送這些資訊,通常加速度計分成兩種:數位和類比,數位加速度計透過序列演算法來作傳送,如:I2C, SPI 或 USART,然而類比加速度計則是輸出事先定義在某個範圍內的電壓值,之後需利用 類比數位轉換器 作轉換,本文中,不會談論到 類比數位轉換器 的轉換細節,除了因為它的範圍太廣,也因為它會隨著不同的平台而有所改變,一些微型控制器擁有內建的類比數位轉換器,而另外一些則需要外部的元件才能作類比數位轉換;不管是哪一種類比數位轉換器,最後都會得到在特定範圍內的數值,舉例來說,一個 10-bit 類比數位轉換器的輸出值會在 0 ~ 1023 之間,1023 是 210 - 1,而 12-bit 類比數位轉換器的輸出值會在 0 ~ 4095 之間,4095 是 212 - 1。
接下來舉一個簡單的例子,假設 10-bit 類比數位轉換器在三軸的輸出值如下:
AdcRx = 586
AdcRy = 630
AdcRz = 561
每個類比數位轉換器都有參考電壓值,假設在本例中為 3.3 V,則轉換 10-bit 類比數位轉換器的輸出值的公式為:
VoltsRx = AdcRx * Vref / 1023
如果是 8-bit 類比數位轉換器,則是除以 255 = 28 - 1,如果是 12-bit 類比數位轉換器,則是除以 4095 = 212 - 1。
將上述的公式代入三軸,可以得到:
VoltsRx = 586 * 3.3V / 1023 = ~1.89V (取到小數點以下兩位)
VoltsRy = 630 * 3.3V / 1023 = ~2.03V
VoltsRz = 561 * 3.3V / 1023 = ~1.81V
每個加速度計都會有零重力電壓標準值,可以在產品規格書中找到,就是在零重力情況下的電壓值,為了要得到正確的電壓值,需要減去零重力情況下的電壓值,假設此例中零重力情況的電壓值為 1.65V,則電壓值減去零重力情況下的電壓值後為:
DeltaVoltsRx = 1.89V - 1.65V = 0.24V
DeltaVoltsRy = 2.03V - 1.65V = 0.38V
DeltaVoltsRz = 1.81V - 1.65V = 0.16V
現在所得到的加速度計的輸出數值單位為伏特,還不是 g(9.8m/s2),為了要作最後的轉換,需要再將加速度計的靈敏度加入計算,靈敏度通常以 mV/g 作為單位,假設此例的靈敏度為 478.5 mV/g = 0.4785 V/g,靈敏度的值也可以在產品規格書中找到,為了將最後的單位轉換為 g,可以使用下列公式:
Rx = DeltaVoltsRx / Sensitivity
Rx = 0.24V / 0.4785V/g = ~0.5g
Ry = 0.38V / 0.4785V/g = ~0.79g
Rz = 0.16V / 0.4785V/g = ~0.33g
當然,也可以將全部步驟包含在一個公式中,之所以會一步一步來是為了能詳細說明如何將類比數位轉換器所測量的數值轉換為以 g 為單位:
Rx = (AdcRx * Vref / 1023 - VzeroG) / Sensitivity (Eq. 2)
Ry = (AdcRy * Vref / 1023 - VzeroG) / Sensitivity
Rz = (AdcRz * Vref / 1023 - VzeroG) / Sensitivity
現在已經將慣性力分解成三個部分,如果這個裝置除了重力之外,沒有受其它力的影響,我們就可以假設這個慣性力的方向就是重力的方向,如果要知道該裝置相對於地平面的傾斜,則可以計算該慣性力向量與Z軸的角度,如果對每一軸的傾斜都感興趣,則可以將結果分成兩部分:在X, Y 軸的傾斜角度如同重力與 X, Y 軸的夾角一樣,是可以被計算出來的,計算這些角度可能會比想像中的還簡單,現在就來計算 Rx, Ry, Rz 的夾角,回到加速度計的模型,並加上角度的標示,如下:
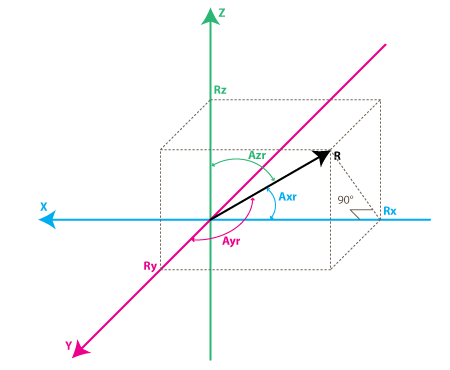
所感興趣的角度為 X, Y, Z 軸與 向量力 R 的夾角,分別定義為 Axr, Ayr, Azr,從上圖可以看到 R 與 Rx 的夾角為:
cos(Axr) = Rx / R,以此類推也可以得到:
cos(Ayr) = Ry / R
cos(Azr) = Rz / R
從 Eq. 1 可以知道 R = SQRT(Rx2 + Ry2 + Rz2)
於是利用 arccos() 函式,就可以得到角度:
Axr = arccos(Rx / R)
Ayr = arccos(Ry / R)
Azr = arccos(Rz / R)
在加速度計的模型上經過漫長的解釋後,所得到的就是上述的幾個公式,需要依據自己的應用程式所需要,再看要使用哪些公式,下文會繼續介紹陀螺儀,也會介紹加速度計與陀螺儀如何結合運作,並提供較正確的傾斜度估計。
在那之前,先看看以下實用的符號表示法:
cosX = cos(Axr) = Rx / R
cosY = cos(Ayr) = Ry / R
cosZ = cos(Azr) = Rz / R
這三個公式稱為方向餘弦,基本上它代表單位向量(向量長度為 1)與 R 向量具有相同的方向,簡單驗証為:
SQRT(cosX2 + cosY2 + cosZ2) = 1
這是一個很好的特性,可以讓我們免除於監視 向量R 的長度,通常如果只對內部向量有興趣,則為了方便計算,可以合理地對這個模組作正規化。
第二部分 陀螺儀
加速度計的第二個模型,同樣可以用來解釋陀螺儀如何在各個軸向作測量:
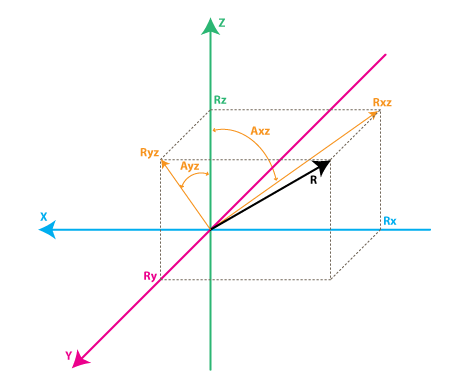
每個陀螺儀頻道測量圍繞著該軸的旋轉,舉例來說,一個二軸陀螺儀會偵測在(或接近) X, Y 軸的旋轉,為了要以數字來表示旋轉,先說明表示法,首先:
Rxz - 向量力 R 在 XZ 平面的投影
Ryz - 向量力 R 在 YZ 平面的投影
在 Rxz 與 Rz 所形成的三角形中,透過畢氏定理可以得到:
Rxz2 = Rx2 + Rz2
相同的方式,也可以得到:
Ryz2 = Ry2 + Rz2
另外,透過畢氏定理也可以得到:
R2 = Rxz2 + Ry2
R2 = Ryz2 + Rx2
本篇文章雖然不會使用到上述的公式,不過明白模型中這些數值彼此間的關係是相當重要的。
接著定義 Z 軸與 Rxz, Ryz 之間的角度關係:
Axz - Rxz(R 在 XZ 平面的投影) 與 Z 軸之間的夾角
Ayz - Ryz(R 在 YZ 平面的投影) 與 Z 軸之間的夾角
陀螺儀就是偵測上述兩個角度的變化速度,換句話說,陀螺儀的輸出數值會與角度的變化速度呈線性相關,舉例來說,假設在 t0 時,繞著 Y軸(也就是Axz角)的旋轉角度為 Axz0,而在 t1 時,該角度變化為 Axz1,則該角度的變化速度為:
RateAxz = (Axz1 - Axz0) / (t1 - t0)
如果 Axz 以角度為單位,而時間以秒為單位,則 RateAxz 的單位為 deg/s,這也就是陀螺儀所量測的數值。
現實上的陀螺儀(除非是特殊的數位陀螺儀)很少會直接給出以 deg/s 為單位的數值,和加速度計一樣,陀螺儀也需要 類比數位轉換器,透過類似於 Eq. 2 的公式,將輸出值轉換為以 deg/s 為單位,陀螺儀的類比數位轉換器轉換公式如下(此例假設是使用 10-bit 類比數位轉換器,如果是 8-bit,則以 255 取代 1023,如果是 12-bit,則以 4095 取代 1023):
RateAxz = (AdcGyroXZ * Vref / 1023 - VzeroRate) / Sensitivity Eq. 3
RateAyz = (AdcGyroYZ * Vref / 1023 - VzeroRate) / Sensitivity
AdcGyroXZ 及 AdcGyroYZ 可以從類比數位轉換器模組取得,分別表示用來測量 向量R 在 XZ 及 YZ 平面投影所形成的旋轉角度的頻道,也就是說旋轉是分別由繞著 Y 及 X 軸轉而形成。
Vref - 為類比數位轉換器參考電壓,上例中以 3.3V 為例子
VzeroRate - 為零速度電壓,也就是在沒有旋轉的情況下所測得的電壓值,以 1.23V 為例 (這個數值可以在產品規格書中找到,不過也不要完全相信產品規格書,因為大部分的陀螺儀在經過焊接後,該數值都會有些微的跳動,所以最好在焊接後,用電壓計重新作測量,通常這個數值在經過焊接後,是不太會有變動的,如果會變動,則需要校正程式在裝置剛開始被啟動時作校正,必須指示使用者在啟動時,把裝置固定住,以完成陀螺儀的校正)。
Sensitivity - 陀螺儀的敏感度,單位為 mV / (deg/s),通常寫為 mV/deg/s,寫表示如果增加 1 deg/s 的旋轉速度,則陀螺儀的輸出值會上升多少 mV,本例中 Sensitivity 的值為 2mV/deg/s 或 0.002V/deg/s。
舉例來說,如果 類比數位轉換器模組回傳的值為:
AdcGyroXZ = 571
AdcGyroYZ = 323
則利用上述公式,可以得到:
RateAxz = (571 * 3.3V / 1023 - 1.23V) / (0.002V/deg/s) = ~306 deg/s
RateAyz = (323 * 3.3V / 1023 - 1.23V) / (0.002V/deg/s) = ~-94 deg/s
也就是說,這個裝置繞著 Y 軸旋轉(或是說繞著 XZ 平面旋轉)的速度為 306 deg/s,而繞著 X 軸旋轉(或是說繞著 YZ 平面旋轉)的速度為 -94 deg/s,負號表示旋轉的方向與正號的方向相反;一個好的陀螺儀規格說明書會說明哪個旋轉方向是正號,否則的話就需要對著裝置作實驗來確定方向,看哪個方向的旋轉會造成輸出電壓值的增加,這部分的測試最好是使用示波器來作,因為在旋轉停止時,輸出的電壓值又會回到零速度電壓值,如果是使用三用電表來作測量,則需要以固定速率旋轉至少數秒,並注意旋轉當下的電壓值,與零速度電壓值作比較,如果旋轉當下的電壓值大於零速度電壓值,則該旋轉方向為正號方向。
第三部分 結合加速度計與陀螺儀
閱讀本文的讀者應該已經取得或是打算取得 IMU 裝置,又或是打算以加速度計與陀螺儀來製作 IMU 裝置。
注意:如果要實作或測試本演算法,可以研讀這篇文章:
Arduino code for IMU Guide algorithm
使用由加速度計與陀螺儀所結合的 IMU 的第一步驟為:對齊他們的座標系統,最簡單的方式是以加速度計的座標系統作為參考基準,大部分的加速度計資料表都會標明該晶片或裝置的 X, Y, Z 軸方向,舉例來說,在 Acc_Gyro 的產品規格說明書中所標示的 X, Y, Z 軸方向為:

接下來的步驟是:
- 確認陀螺儀的輸出數值,如之前所提到的 RateAxz 與 RateAyz
- 判斷這些輸出數值是否需要作座標系統的轉換,因為陀螺儀與加速度計的軸向未必會相同
就算是在同一顆 IMU 中,也不要假設陀螺儀的輸出值的軸向一定會與加速度計的軸向相同,最好的方向是自行測試,來確定軸向是否相同。
這裡提供範例步驟來決定哪一個陀螺儀的輸出值會對應到上述所提到的 RateAxz:
- 一開始把裝置以水平放置;加速度計的 X, Y 軸向的值為零重力電壓值 (以Acc_Gyro為例,其值為 1.65V)
- 接著將此裝置對著 Y 軸作旋轉,也就是對著 XZ 平面旋轉,所以 X, Z 的加速度值會跳動,但 Y 軸的值不會改變
- 轉動此裝置的同時,其陀螺儀的某個軸向的輸出值會改變,其它軸向不會變動
- 輸出值會改變的那個軸向為對著 Y 軸旋轉(對 XZ 平面旋轉)的輸出值,也就是 AdcGyroXZ 的值,可以用來計算 RateAxz
- 最後一個步驟為判斷旋轉方向,因為陀螺儀與加速度計的相對位置的關係,有時候必須反轉 RateAxz 的數值
- 重覆作一開始的測試,對著裝置的 Y 軸作旋轉,並觀察加速度計的 X 軸輸出值的變化(本範例的 AdcRx),如果 AdcRx 的值愈來愈大(從一開始的水平位置旋轉到 90° 的位置),則 AdcGyroXZ 的輸出值應該是愈來愈小,這是因為被觀察的值是重力向量,當裝置往某個方向旋轉時,該動力向量會往相反方向旋轉(相對於被旋轉裝置),如果不是這樣,則需要反轉 RateAxz 的輸出值,可以利用在 Eq. 3 加上正負號的判斷來完成:
RateAxz = InvertAxz * (AdcGyroXZ * Vref / 1023 - VzeroRate) / Sensitivity
其中 InvertAxz 的值為 1 或 -1
相同的測試,也可以決定 RateAyz 的值,經由對裝置的 X 軸旋轉,可以決定 RateAyz 是對應於哪個陀螺儀的輸出值,以及該輸出值是否需要被反轉,只要取得 InvertAyz 的值後,就可以利用以下公式計算 RateAyz:
RateAyz = InvertAyz * (AdcGyroYZ * Vref / 1023 - VzeroRate) / Sensitivity
如果是在 Acc_Gyro 上作測試,可以得到如下結果:
- RateAxz 的輸出針角是 GX4 且 InvertAxz = 1
- RateAyz 的輸出針角是 GY4 且 InvertAyz = 1
到此,目前的 IMU 裝置應該可以正確計算出 Axr, Ayr, Azr(如第1部分 加速度計所定義),以及 RateAxz, RateAyz(如第2部分 陀螺儀所定義),接下來會繼續分析這些數值間彼此的關係,由結果証明這些關係對於取得裝置相對於地平面之間的更準確傾斜角度是相當有幫助的。
想想這個問題,如果加速度計已經可以算出 Axr, Ayr, Azr 的傾斜角度,為何還需要陀螺儀的測量值呢?答案很簡單,因為加速度計的量測結果是不能百分百被信任的,原因有許多個,其中之一為加速度計測量的是慣性力,該慣性力會被重力所影響(理想情況下是只受重力影響),但它也可能受該裝置的加速度(移動)影響,而就算是加速度計處於相對穩定的狀態,它對於振動及雜訊也相當敏感,這就是為什麼大部分的 IMU 系統會使用陀螺儀來消除加速度計錯誤的原因,但這該如何實作呢?又難道陀螺儀就沒有雜訊嗎?
陀螺儀的測量結果也是會有雜訊,但因為陀螺儀測量的是旋轉角度,所以較不容易受線性移動的影響,而加速度計卻被線性移動影響,但陀螺儀也是有其它問題,舉例來說,其中之一是漂移(在旋轉停止時,陀螺儀的輸出值不會馬上回到零速度值),然而對於裝置的傾斜度估計,透過將加速度計與陀螺儀的測量值作平均與只使用加速度計的測量值相比較,前者可以得到相對較佳之估計。
接下來所介紹的演算法是受某些實作於卡爾曼濾波器的觀念所啟發而想到的,但是簡單許多,且易於實作在嵌入式系統,這個演算法首先要計算的是重力向量 R = [Rx, Ry, Rz] 的方向,並從中推導出 Axr, Ayr, Azr 及 cosX, cosY, cosZ ... 等,這將提供該裝置相對於地平面的傾斜狀況,這些已在第一部分作過介紹,可能有人會提出疑問,在第一部分的 Eq. 2 不是已經有計算出 Rx, Ry, Rz 的值了嗎? 說的沒錯,但這些值是單純由加速度計所計算出來,如果直接使用,它所包含的雜訊可能會超過應用程式所能負荷,為了避免造成困擾,以下重新定義加速度計的測量值:
Racc - 由加速度計算測量到的慣性力向量,包含下列分量 (在 X, Y, Z 軸的投影):
RxAcc = (AdcRx * Vref / 1023 - VzeroG) / Sensitivity
RyAcc = (AdcRy * Vref / 1023 - VzeroG) / Sensitivity
RzAcc = (AdcRz * Vref / 1023 - VzeroG) / Sensitivity
於是單純從加速度計來看,可以得到一組測量值,這組測量值可以稱為向量,表示法為:
Racc = [RxAcc, RyAcc, RzAcc]
也因為這組測量值可以只由加速度計取得,可以將這組值視為所要介紹的演算法的輸入值。
也因為 Racc 主要是測量重力,所以可以假設這組向量的長度為 1,定義如下:
|Racc| = SQRT(RxAcc2, RyAcc2, RzAcc2)
因此可以將這組向量的表示法更新為:
Racc(正規化) = [RxAcc/|Racc|, RyAcc/|Racc|, RzAcc/|Racc|]
這將確保正規化後的 Racc 的長度值必定為 1。
接著定義一組新向量為:
Rest = [RxEst, RyEst, RzEst]
這會是該演算法的輸出值,並且已經以陀螺儀的量測值及之前的預測值作過修正。
演算法的步驟如下:
- 由加速度計可以得知:目前裝置的位置為 Racc
- 回覆:謝謝,我會確認看看
- 利用陀螺儀的資訊及之前的預測值來修正 Racc,進而得到最新預測的 Rest
- 將 Rest 視為表示裝置目前位置的最佳值
接著介紹實作這個演算法的方式。
最一開始的步驟是信任加速度計的測量值,設定:
Rest(0) = Racc(0)
因為 Rest 與 Racc 都是向量值,所以上述的簡單表示法其實是三組值的設定:
RxEst(0) = RxAcc(0)
RyEst(0) = RyAcc(0)
RzEst(0) = RzAcc(0)
接著,會持續規律地每間隔 T 秒就作測量,並得到測量值 Racc(1), Racc(2), Racc(3), ...,同時也將這些測量值指定給 Rest(1), Rest(2), Rest(3), …。
假設現在在第n個步驟,此時會有兩組已知的數值供參考使用:
Rest(n-1) - 前一個步驟的預測值,其中 Rest(0) = Racc(0)
Racc(n) - 目前加速度計的測量值
在計算 Rest(n) 之前,先介紹另一組預測值,是由陀螺儀的測量值與前一個預測值所計算而得。
這個值稱為 Rgyro,它有三個分量:
Rgyro = [RxGyro, RyGyro, RzGyro]
以下先從計算 RxGyro 的方式開始介紹。
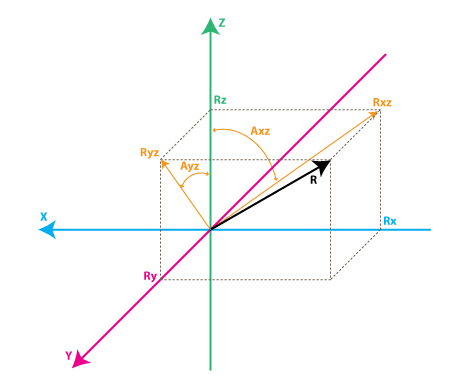
從上圖中的陀螺儀模型來看,從右側由 Rz 及 Rxz 形成的直角三角形可以推導出:
tan(Axz) = Rx / Rz => Axz = atan2(Rx, Rz)
可能有人沒看過 atan2 這個函式,atan2 相似於 atan,只是它需要兩個參數,回傳值範圍為 (-PI, PI),而 atan 只需要一個參數,且回傳值範圍為 (-PI/2, PI/2),這使得在將 Rx, Rz 的值轉換成角度時,可以得到 360 度的完整範圍,進一步的資訊可以參考 atan2。
所以在得知 RxEst(n-1) 及 RzEst(n-1) 後,可以計算:
Axz(n-1) = atan2(RxEst(n-1), RzEst(n-1))
又因為陀螺儀的值是計算 Axz 夾角的變化速度,所以可以預估 Axz(n) 的新角度為:
Axz(n) = Axz(n-1) + RateAxz(n) * T
RateAxz 的值可以由陀螺儀的類比數位轉換器取得,較為精準的公式可以取平均速度來作計算:
RateAxzAvg = (RateAxz(n) + RateAxz(n-1)) / 2
Axz(n) = Axz(n-1) + RateAxzAvg(n) * T
同樣的推導,也可以得到:
Ayz(n) = Ayz(n-1) + RateAyz(n) * T
所以目前所得到的值有 Axz(n) 及 Ayz(n),接下來要如何利用這兩個值來求 RxGyro 及 RyGyro? 從 Eq. 1 可以知道陀螺儀向量的長度可以表示為:
|Rgyro| = SQRT(RxGyro2 + RyGyro2 + RzGyro2)
也因為對 Racc 向量作正規化的關係,同樣可以假設陀螺儀向量的長度為 1,而且不會因為旋轉而改變,因此可以寫為:
|Rgyro| = 1
以下的推導過程將暫時使用如下的簡單標記法:
x = RxGyro, y = RyGyro, z = RzGyro
綜合上述關係,可以寫成:
x = x / 1 = x / SQRT(x2 + y2 + z2)
將分子與分母同除以 SQRT(x2 + z2):
x = (x / SQRT(x2 + z2)) / SQRT((x2 + y2 + z2) / (x2 + z2))
其中 x / SQRT(x2 + z2) = sin(Axz):
x = sin(Axz) / SQRT(1 + y2 / (x2 + z2))
將 SQRT 內的分子與分母同乘 z2:
x = sin(Axz) / SQRT(1 + y2 * z2 / (z2 * (x2 + z2))
又因為 z / SQRT(x2 + z2) = cos(Axz) 且 y / z = tan(Ayz):
x = sin(Axz) / SQRT(1 + cos(Axz)2 * tan(Ayz)2)
回到最初所使用的符號,可以得到:
RxGyro = sin(Axz(n)) / SQRT(1 + cos(Axz(n))2 * tan(Ayz(n))2)
利用類似的推導,也可以得到:
RyGyro = sin(Ayz(n)) / SQRT(1 + cos(Ayz(n))2 * tan(Axz(n))2)
要進一步簡化此公式也是可以的,再將分子與分母同除以 sin(Axz(n)):
RxGyro = 1 / SQRT(1 / sin(Axz(n))2 + cos(Axz(n))2 / sin(Axz(n))2 * tan(Ayz(n))2)
RxGyro = 1 / SQRT(1 / sin(Axz(n))2 + cot(Axz(n))2 * sin(Ayz(n))2 / cos(Ayz(n))2)
接著先加上再減去 cos(Axz(n))2 / sin(Axz(n))2 = cot(Axz(n))2:
RxGyro = 1 / SQRT(1 / sin(Axz(n))2 - cos(Axz(n))2 / sin(Axz(n))2 + cot(Axz(n))2 * sin(Ayz(n))2 / cos(Ayz(n))2 + cot(Axz(n))2)
先結合第1,2 項,再結合第3,4項:
RxGyro = 1 / SQRT(1 + cot(Axz(n))2 * (1 + tan(Ayz(n))2)
RxGyro = 1 / SQRT(1 + cot(Axz(n))2 * (sec(Ayz(n))2)
這個公式只用到兩個三角函數,可以增加計算速度,如果有興趣,可以自行用程式確認跟進一步簡化前的公式相比,其執行速度是否有比較快。
最後,可以得到:
RzGyro = Sign(RzGyro) * SQRT(1 - RxGyro2 - RyGyro2)
其中,如果 RzGyro >= 0,則 Sign(RzGyro) = 1,又如果 RzGyro < 0,則 Sign(RzGyro) = -1
有一個簡單的預估方式為:
Sign(RzGyro) = Sign(RzEst(n-1))
在實作上,如果 RzEst(n-1) 驅近於 0 的情況,則或許可以考慮跳過上述整個參考陀螺儀的輸出數值的步驟,直接設定: Rgyro = Rest(n-1),Rz 的值會在計算 Axz 及 Ayz 的角度時被參考使用,當 Rz 驅近於 0,可能會造成溢位或是其它不好的結果,例如陷在相當大的浮點數中,而其中的 tan() / atan() 可能已經失去準備度。
重新整理目前所擁有的資訊,目前在第 n 個步驟,已經計算出下列數值:
Racc - 目前加速度計的輸出值
Rgyro - 從上一個估測值及目前陀螺儀的輸出值所計算
至於是哪個數值會被用來更新 Rest(n) 呢? 你可能已經猜到了,兩個都會被使用,使用方式為加權平均:
Rest(n) = (Racc * w1 + Rgyro * w2) / (w1 + w2)
簡化此公式,分子、分母同除以 w1:
Rest(n) = (Racc + Rgyro * w2 / w1) / (1 + w2/w1)
將 w2/w 以 wGyro 取代:
Rest(n) = (Racc + Rgyro * wGyro) / (1 + wGyro)
上述公式 wGyro 的值代表相對於加速度計來說,有多信任對於陀螺儀的輸出數值,從實驗數據來看,這個數值的選擇如果在 5 ~ 20 之間,通常會有不錯的效果。
上述演算法與卡爾曼濾波器的相異之處在於權重值是否固定,在卡爾曼濾波器中,權重值是會根據加速度計的雜訊強度而一直被更新的,卡爾曼濾波器的重點在於提供理論上的最佳結果,然而上述的演算則是在於提供"能用就好"的結果,讀者也可以自行實作根據雜訊強度來調整 wGyro 的值,只是固定的 wGyro,應該已經可以符合大部分應用程式的需求。
距離更新估測值似乎還差最後一個步驟:
RxEst(n) = (RxAcc + RxGyro * wGyro) / (1 + wGyro)
RyEst(n) = (RyAcc + RyGyro * wGyro) / (1 + wGyro)
RzEst(n) = (RzAcc + RzGyro * wGyro) / (1 + wGyro)
再將這個向量作正規化:
R = SQRT(RxEst(n)2 + RyEst(n)2 + RzEst(n)2)
RxEst(n) = RxEst(n) / R
RyEst(n) = RyEst(n) / R
RzEst(n) = RzEst(n) / R
接著,可以繼續往下作第 n+1 個階段的估測。
注意:如果要實作或測試本演算法,可以研讀這篇文章:
Arduino code for IMU Guide algorithm
Reference
A Guide To using IMU (Accelerometer and Gyroscope Devices) in Embedded Applications.
文字內容 或 影像內容 部份參考、引用自網路,如有侵權,請告知,謝謝。
全站熱搜


 留言列表
留言列表
