卡爾曼濾波器 (Kalman Filter) 是一篇在 1960年由 Kalman 本人所提出的博士論文,主要的功能為預估動態系統的狀態。
Kalman Filter 的五個公式為:
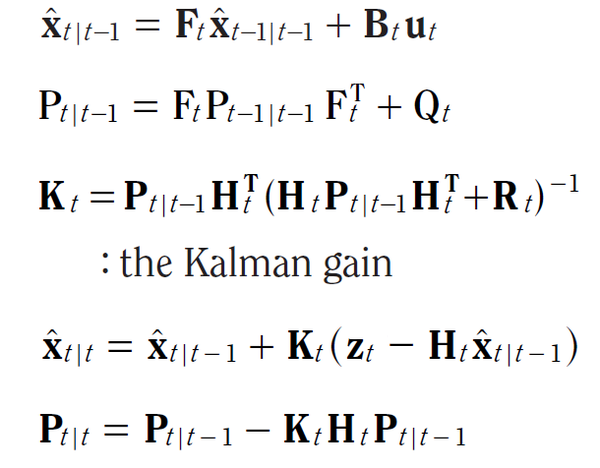
以下開始為英翻中的內容,事先聲明:目前對 Kalman Filter 也只是初學階段,如有翻譯、解釋錯誤之處,再請見諒,並請指教、告知,謝謝。
通過簡單且直覺的推導瞭解 Kalman Filter 的基礎
本文針對 Kalman Filter 提供一個簡單且直覺的推導,主要的目的是為了讓數學背景不夠的讀者 ,可以輕鬆瞭解這個有用的工具。本文中,所用到最複雜的數學為兩個高斯函數(Gaussian function) 的乘法,並簡化其相乘後的結果。
自 Kalman Filter 被提出以來,已經超過 50 多年,至今它仍然是目前普遍用來作 資料融合(data fusion) 的重要演算法之一。Kalman Filter 的成功在於所需要的計算量小、優美的遞迴特性以及對一維的線性系統來說,在高斯錯誤統計(Gaussian error statistics) 的情況下,它是最理想的預測器。Kalman Filter 所用來處理的典型問題包括: 平滑具有雜訊的資料 以及 提供參數預測; 其應用範圍很廣,包含: 全球定位系統(GPS) 的接收器、無線電系統的 鎖相環(Phase-Locked Loop)、筆電上的觸控板…等。
以理論上的觀點來說,如果存在某個線性動態系統是一個 貝式模型(Bayesian Model) - 相似於 隱馬可夫模型(Hidden Markov Model),但所有潛在參數的 狀態空間(state space) 皆為連續,且所有的潛在參數和可見參數皆為 高斯分佈(Gaussian Distribution) (通常來說會是 多變數高斯分佈 (multivariate Gaussian Distribution)),則透過 Kalman Filter 的演算法,可以在這個線性動態系統中,得到精確的推斷結果。如果對這段描述覺得有點困惑或有點嚇人,這篇文章的目的就是希望可以利用簡單、直覺的推導,讓大家瞭解 Kalman Filter 的基礎。
相關性 [RELEVANCE]
在資訊處理的領域中,Kalman Filter (及其變型: Extended Kalman Filter 及 Unscented Kalman Filter) 是最負盛名及最受歡迎的 資料融合(data fusion) 演算法;最出名的應用是在阿波羅計劃的導航系統中,將 阿姆斯壯(Neil Armstrong) 送上月球及(更重要地)送回地球;目前來說,在每個衛星導航裝置、每台智慧型手機以及很多電腦遊戲中,都存在著 Kalman Filter。
典型的 Kalman Filter 推導,是以 向量代數(vector algebra) 作為 最小均方估計器(Minimum Mean Squared Estimator) ,這個方法很適合數學能力較強的讀者,但對於數學能力不足的,則不容易理解。本文中對 kalman Filter 的推導,遵守的第一準則為:考慮一個自然界中的例子,並利用 高斯分佈(Gaussian Distribution) 的特性,來對 Kalman Filter 作推導,更明確的說,是利用兩個高斯分佈的函數相乘,其乘積結果,仍然是一個高斯分佈的函數。
前提 [PREREQUISITES]
這篇文章並不是對沒有任何概念的讀者,作一個通盤的 Kalman Filter 介紹,而是以簡單的方法,對非具有深厚數學背景的讀者,介紹 Kalman Filter 的基本概念。本篇文章的基本假設為讀者已經熟悉 向量符號(vector notation) 以及與 Kalman Filter 相關的術語, 如:狀態向量(state vector)、共變異數矩陣(covariance matrix),本文的目標讀者為:需要以簡單且直覺的方式向別人教授 Kalman Filter 或是對 Kalman Filter 有使用經驗,但不完全瞭解其基礎的人,本文的目標不是對初學者教授完整 Kalman Filter 的概念,因為那需要一個章節來解說,而不只是短短幾頁。
問題描述 [PROBLEM STATEMENT]
在 Kalman Filter Model 中,假設系統在時間 t 的狀態可以由系統在時間 t-1 時的狀態所演變而來,其演變的方程式為:
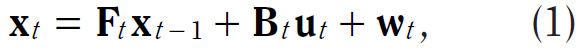
其中:
- xt 為狀態向量,包含系統在時間 t 時,所感興趣的項目,如:位置、速度、方向。
- ut 為控制參數的向量,如:轉向的角度、油門設定、剎車力道。
- Ft 為狀態轉換矩陣,用來將系統在時間 t-1 時的狀態參數轉換成在時間 t 時,對系統所造成的影響,如:在時間 t-1 時的位置及進度,會影響系統在時間 t 時的位置及速度。
- Bt 為控制參數矩陣,用來將在 ut 中的控制參數轉換對系統的狀態向量所造成的影響,如:將油門設定,轉換成對速度及位置的影響。
- wt 由狀態向量中,每個參數的 程序雜訊值(Process Noise) 所構成的向量;程序雜訊假設為 零均值多元的常態分佈(Zero Mean Multivariate Normal Distribution),其 共變異數(Covariance) 由 共變異數矩陣(Covariance Matrix) - Qt 提供。
如果要對該系統作測量,可以利用下列模型:
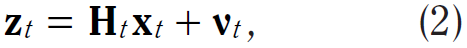
其中:
- zt 為測量值向量。
- Ht 為將狀態向量參數對映到測量領域的轉換矩陣。
- vt 由所有測量參數的雜訊所構成的向量,和程序雜訊相同,測量雜訊同樣被假設為零均值高斯白雜訊,其共變異數為 Rt
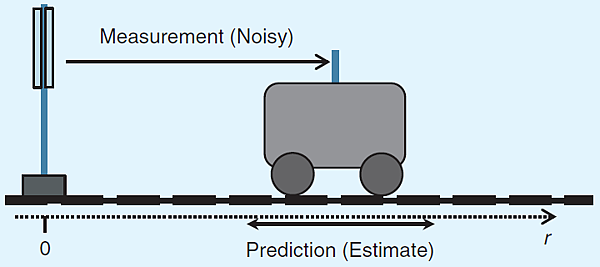
圖一,在一維系統的考量下。
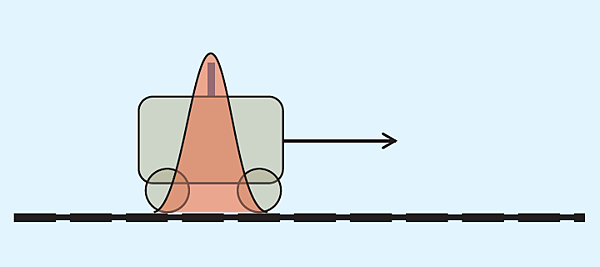
圖二,系統在 t = 0 的情況下,紅色的高斯分佈代表機率密度函數對火車位置的最初預估的信心值;箭頭表示已知的最初火車速度。
在接下來的推導中,將以簡單的一維追蹤作為例子,有點類似於火車在鐵軌上行走的情況 (如圖一);考量此問題中的向量與矩陣之值,其狀態向量 xt 包含火車的位置與速度:
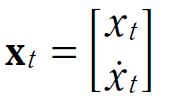
火車司機也可能剎車或加速,假定其力道的強度為 ft,火車的重量為 m,則儲存在控制向量 ut 的值為:
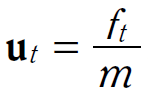
在 Δt(從 t-1 到 t) 期間,火車的剎車或加速力道與其位置與速度的關係為:
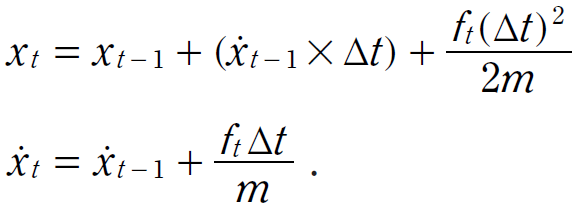
上述的線性方程式可以以矩陣方式改寫為:
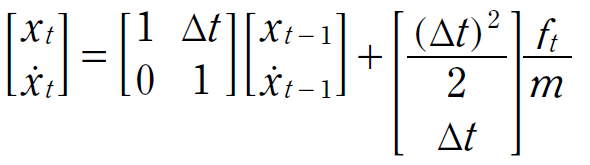
和公式(1) 對照,在此例子中,可以得到:
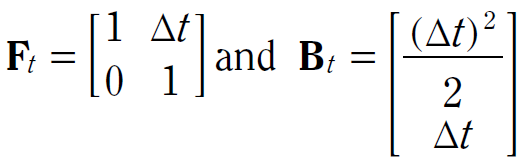
因為系統中,其 xt 的真實狀態無法靠直接觀察而得知,所以 Kalman Filter 提供相關演算法,經由結合系統模型及測量到的參數模型或線性參數模型,來決定 x̂t 的值。在狀態向量中,所預測的參數值會以 機率密度函數(Probability Density Function, pdf) 來表示,而不是明確的數字。有關 Kalman Filter 是以 高斯機率密度函數(Gaussian pdfs) 為基礎這部分,會在 - 問題解決[SOLUTIONS] 中作較清楚的說明。
為了要完整描述高斯函數,需要知道相關的變異數及共變異數,這些數值儲存在 共變異數矩陣(Covariance Matrix) Pt 中,Pt 的對角線元素是狀態向量的變異數,而其它非對角線元素,則是狀態向量之間的共變異數。一維線性系統中,在測量值的誤差為零均值高斯分佈的情況下,Kalman Filter 可以說是最完美的預估器 [1]。
接下來的章節,會推導 Kalman Filter 的方程式,這些方程式結合上述的資訊、系統模型的預測值及測量誤差值,以遞迴的方式算出 x̂t。
Kalman Filter 的演算法包含兩個步驟:預估 與 測量修正。在預估階段的標準 Kalman Filter 方程式為:
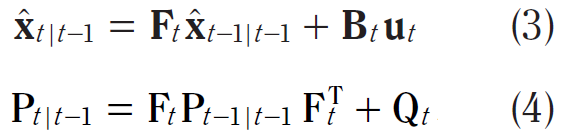
其中 Qt 為和控制輸入的雜訊有關的程序雜訊共變異數矩陣,算式(3) 已經在前文中作了明確的推導,這邊開始作算式(4) 的推導,假設在預估值 - x̂t|t-1 與未知的真實值 xt 之間的相關變異數為:
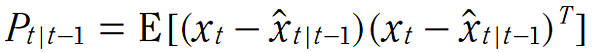
接著將 算式(1) 與 算式(3) 相減,得到:
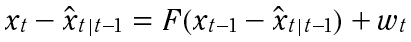
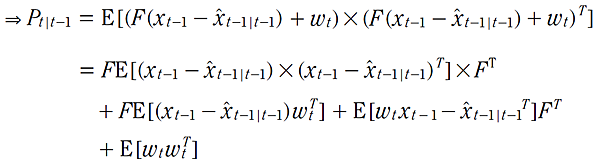
需注意 狀態預測錯誤值(State Estimation Errors) 與程序噪音為 無關聯(uncorrelated),故:
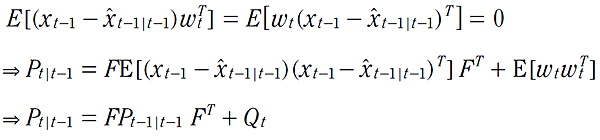
到此預估階段的推導結束。
測量修正階段的方程式為:
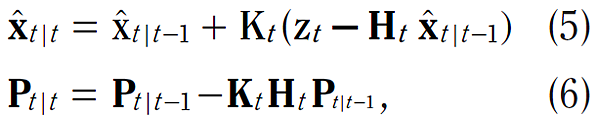
其中:
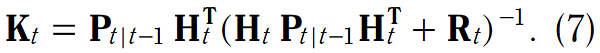
在本文餘下的部分,會根據第一準則來推導方程式 (5) - (7)。
問題解決 [SOLUTIONS]
這邊會以簡單的一維追蹤的條件下,對 Kalman Filter 的推導,更精確的來說,也就是火車在軌道上的移動。在每次的測量期間,希望可以對火車的位置作最可能的預測 (或更精確的說,是天線在火車上所安裝的位置)。相關訊息的來源可以是:1) 利用上次火車的位置及速度來作預估 及 2) 利用火車上的天線作測量。預估及測量到的資訊將會被結合在一起,以期待提供對火車位置的最佳預測,整個系統如圖一所示。
在合理的精確度下,可以得知系統的最初 (在 t = 0 時) 狀態 ,如圖二,火車的位置是以高斯機率密度函數提供,可以根據 t = 0 時的火車位置、速度及最大的可能加速度、減速度,來預估下一個時間點(t = 1) 時的火車位置。實際上,應該可以知道駕駛對火車的加速或減速的控制,在任何情況下,都可以對火車接下來的位置作預估,如圖三所示,以具有不同均值及變異數的新的高斯機率密度函數表示;數學上,這個步驟是以算式(1) 代表。隨著變異數的增加(參考算式(2)),代表對於位置的預估的精確度會跟著減少,因為在 t = 0 及 t = 1 之間的加速度或減速度的測量上,都會有程序噪音的存在。
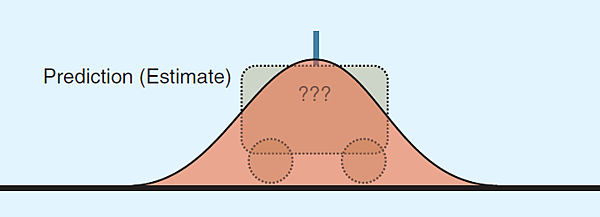
圖三,在 t = 1 時,對於火車位置的預估,不確定性的程度如圖,對於所預估的結果信心度減少,因為不確定在 t = 0 到 t = 1 之間,是否有發生加速或減速的情況。
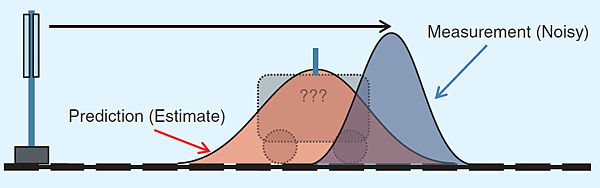
圖四,在 t = 1 時,對於火車位置的測量,因為在測量時,可能會受雜訊影響,其不確定性由藍色的高斯機率密度函數表示;在此系統中,要結合此兩個機率密度函數的方式是將它們相乘。
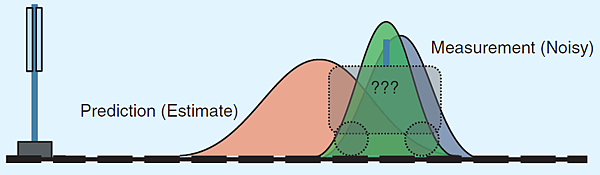
圖五,新的(綠色)機率密度函數是在 t = 1 時,由預估及測量所得到的兩個機率密度函數相乘的結果;這個新的機率密度函數藉由結合預估和測量,進而提供火車位置的最佳預測結果。
在 t = 1 時,也可以利用無線定位系統對火車的位置進行測量,如圖四中的藍色高斯機率密度函數;而對火車位置的最佳預測,可以由結果預估和測量的結果所得,結合的方式為將兩者相關的機率密度函數相乘,如圖五中,綠色機率密度函數所示。
這邊用到一個很重要的高斯函數的特性:兩個高斯函數相乘所得到的乘積是另一個高斯函數。這個特性的關鍵在於它允許高斯機率密度函數可以隨著時間而無窮盡的相乘,而相乘後的結果不會導致複雜度或項目的增加;在每個時間間隔後,這個新的機率密度函數就代表著高斯函數。這也是 Kalman Filter 所存在優美遞迴的主要原因。
接著將以數學的觀點,重新回到上述所討論的圖形的狀態,來推導 Kalman Filter 在測量修正階段的算式。
預估階段的機率密度函數,如圖三中的紅色高斯函數所示,其方程式為:
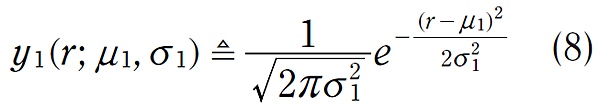
測量階段的機率密度函數,如圖四中的藍色高斯函數所示,其方程式為:
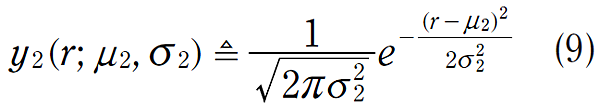
結合這兩個機率密度函數的方式為將他們相乘,也就是同時考慮預估與測量 (如圖五);這個新的機率密度函數代表預估階段與測量階段的資訊融合,因此,對於系統的最佳預測就是這兩個高斯函數的乘積:
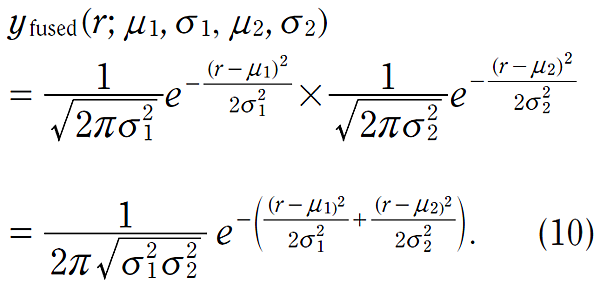
在這個新函數的2次方的項目,可以被擴展,所以整個表示式,可以以高斯型式改寫為:
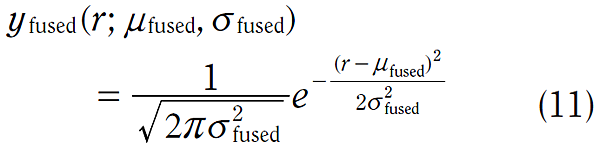
其中:
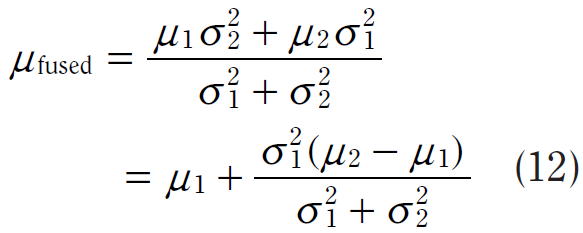
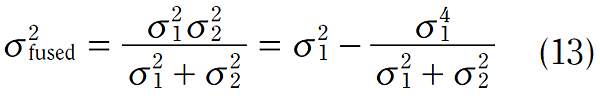
最後兩個方程式代表 Kalman Filter 演算法中的測量修正階段,會在下文中作詳述,然而為了要展示更為通用的情況,需要先將上述範例作延伸。
上述範例中,是假設在預估及測量階段都是使用同一座標體系,且具有相同的單位,所以可以在預估及測量修正階段得到相當精準的算式。然而要注意的是在現實中,常常還需要額外的步驟將預估值與測量值對映到同一個值域。將上述的範例延伸為更真實的情況,對於火車位置的預估是在鐵軌中的移動距離,以公尺為單位。但無線電波的測量則是以秒為單位。為了要讓預估值與測量值可以相乘,其中一個必須轉換到與另一個相同的值域,而其標準作法就是將預估值透過 轉換矩陣(Transformation Matrix) Ht 轉換到測量值域。
回到算式(8)、(9),不再允許 y1 及 y2 皆以火車軌道的距離為單位,將 y2 的值,以無線電波訊號從目前位置飛行到 t = 0 時火車的位置,所需的飛行時間作考慮,所以 y1 在空間域的預測,在除以光速-c 後,即轉換到測量值域。算式(8)、(9)可以改寫為:
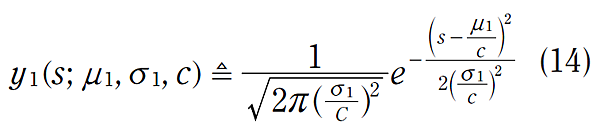
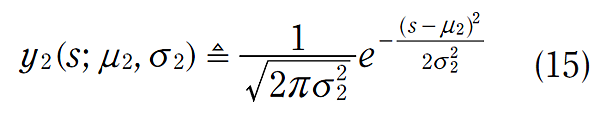
算式中,兩個值域的分佈皆為測量值域,也就是無線電波在時間軸傳播的值,以秒為單位。
根據之前的推導,可以得到:
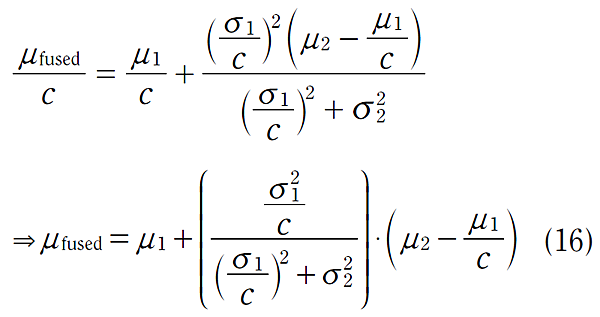
以 H = 1/c 及 K = (Hσ12)/(H2σ12 + σ22) 來取代,可以得到:
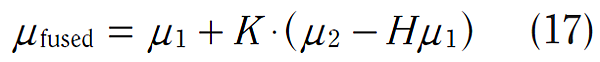
相同的,在預測值中,經融合後的變異數變成:
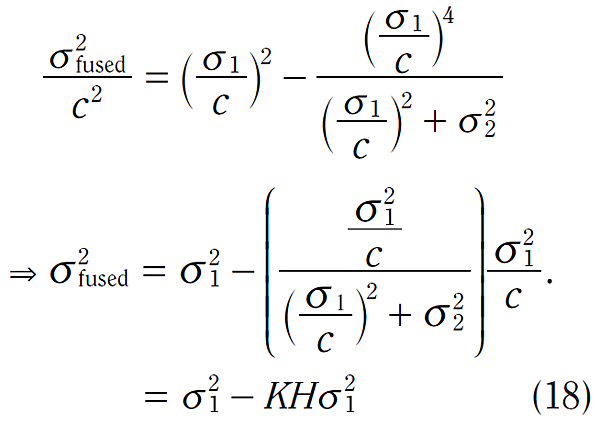
現在可以對這個純量推導的某些項目與 Kalman Filter 演算法中的標準向量與矩陣作比較:
μfused → x̂t|t:經資料融合後的狀態向量
μ1 → x̂t|t-1:資料融合之前的狀態向量,也就是預估值
σfused2 → Pt|t:經資料融合後的 共變異數矩陣(信心值)
σ12 → Pt|t-1:資料融合之前的 共變異數矩陣(信心信)
μ2 → zt:測量向量
σ22 → Rt:存在於測量值之雜訊的 不確定性矩陣(Uncertainty Matrix)
H → Ht:轉換矩陣,用來將狀態向量的參數轉換到測量值域
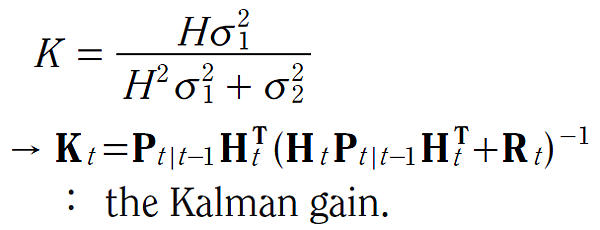
現在即可簡單看出標準的 Kalman Filter 方程式與 算式(17)(18) 之間的關係:
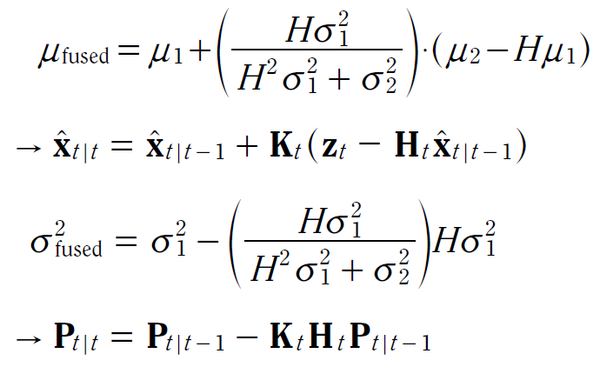
結論 [CONCLUSION]
Kalman Filter 可以經過簡單的推導來教授 ,其推導包括:純量數學、基本代數操作以及簡單的實驗。這個方式應該可以讓缺乏堅強數學背景的讀者,透過直覺的方式,理解 Kalman Filter 的數學核心 以及 透過高斯函數獨特的乘法特性,瞭解 Kalman Filter 的遞迴性質。
Kalman Filter 相關文章
Understanding the Basis of the Kalman Filter Via a Simple and Intuitive Derivation
卡爾曼濾波 (Kalman Filter)
Reference
Understanding the Basis of the Kalman Filter Via a Simple and Intuitive Derivation
文字內容 或 影像內容 部份參考、引用自網路,如有侵權,請告知,謝謝。
全站熱搜


 留言列表
留言列表
