探討在二維平面上的點,經旋轉特定角度後,其 位置(二維座標) 變化該如何計算。
探討在三維空間中的點,經旋轉特定角度後,其 位置(三維座標) 變化該如何計算。
平面上的旋轉
假設在平面上有一點 (x, y),則以原點為中心,逆時針方向旋轉 θ 後,其座標 (x', y') 與 原座標點 (x, y) 的關係為:
x' = cos(θ) * x - sin(θ) * y
y' = sin(θ) * x + cos(θ) * y
以矩陣表示為:

旋轉矩陣的由來可以從 三角函式 或是 單位向量 兩個方向來推導。
三角函式的推導
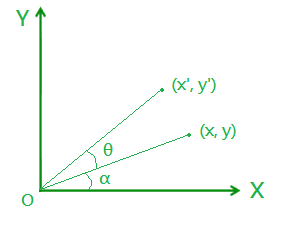
令 r2 = x2 + y2,且 r > 0,則:
x = r * cos(α),y = r * sin(α)
x' = r * cos(α+θ),y' = r * sin(α+θ)
根據合角公式:
sin(α+θ) = sin(α)cos(θ) + cos(α)sin(θ)
cos(α+θ) = cos(α)cos(θ) - sin(α)sin(θ)
重新得到 x' 及 y':
x' = r * (cos(α)cos(θ) - sin(α)sin(θ)) = r * cos(α)cos(θ) - r * sin(α)sin(θ)
y' = r * (sin(α)cos(θ) + cos(α)sin(θ)) = r * cos(α)sin(θ) + r * sin(α)cos(θ)
將 x = r * cos(α),y = r * sin(α) 代入,可以得到 (x, y) 與 (x', y') 之間的關係:
x' = cos(θ) * x - sin(θ) * y
y' = sin(θ) * x + cos(θ) * y
單位向量的推導
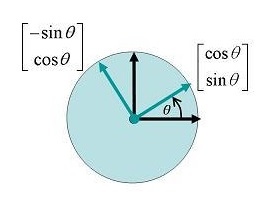
在二維平面上,其單位向量為:
e1 = [1, 0], e2 = [0, 1]
分別旋轉 θ 後,其位置的變化分別為:
T(e1) = [cosθ, sinθ], T(e2) = [-sinθ, cosθ]
所以其旋轉矩陣為:
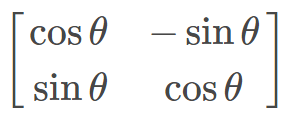
空間中的旋轉
在三維座標軸的旋轉中,可以將其旋轉分解成三個部分,也就是分別對 X, Y, Z 軸的旋轉,假設對 Y, X, Z 軸的旋轉角度分別為 θy, θx, θz,其旋轉矩陣表示法可以為:
R = RY(θy)RX(θx)RZ(θz)
在單獨對 Z 軸旋轉的情況下,該三維座標點的座標轉換只對 X, Y 平面有影響,也就是 X, Y 平面旋轉:
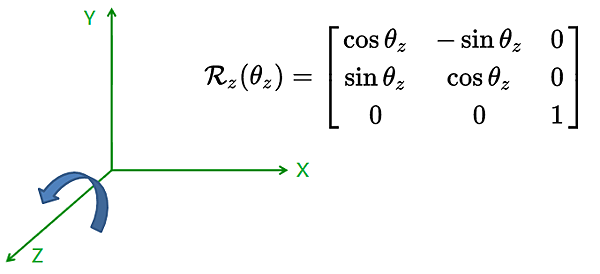
在單獨對 X 軸旋轉的情況下,該三維座標點的座標轉換只對 Y, Z 平面有影響,也就是 Y, Z 平面旋轉:
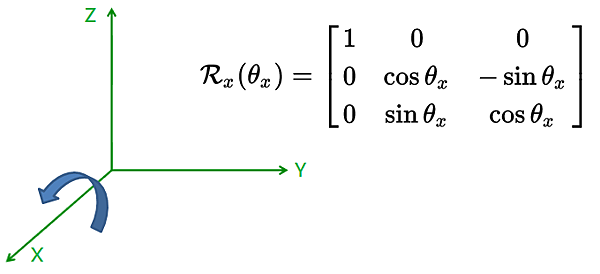
在單獨對 Y 軸旋轉的情況下,該三維座標點的座標轉換只對 X, Z 平面有影響,也就是 X, Z 平面旋轉:
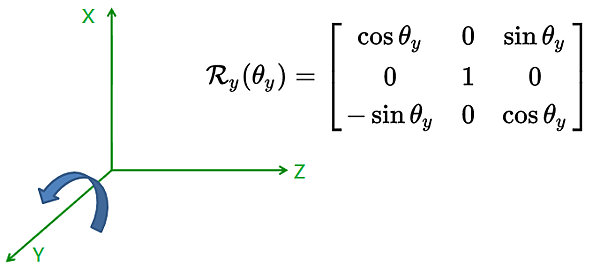
在 R = RY(θy)RX(θx)RZ(θz) 的前提下:
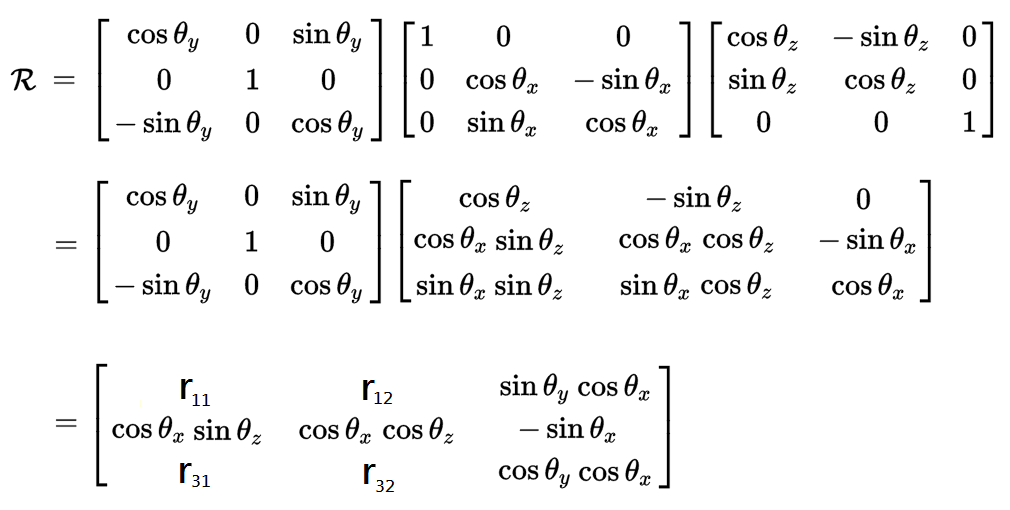
從最後已經作完乘法的旋轉矩陣來看,如果要分別求得 θy, θx, θz ,其計算方式為:
θy = arctan(r13 / r33)
θx = arcsin(-r23)
θz = arctan(r21 / r22)
也就是說,只要有旋轉矩陣 R,就可以進行運算,個別得到對 X, Y, Z 軸的旋轉角度: θx, θy, θz。
而如果在 R = RZ(θz)RX(θx)RY(θy) 的前提下,旋轉矩陣為:
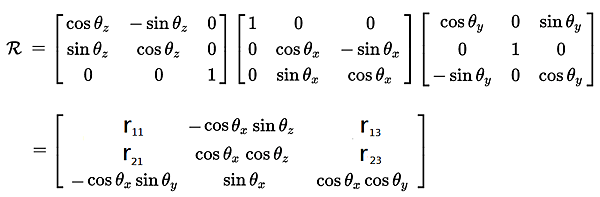
其中:
r11 = cos(θy)cos(θz) - sin(θx)sin(θy)sin(θz)
r13 = sin(θy)cos(θz) + sin(θx)cos(θy)sin(θz)
r21 = cos(θy)sin(θz) + sin(θx)sin(θy)cos(θz)
r23 = sin(θy)sin(θz) - sin(θx)cos(θy)cos(θz)
補充 - 歐拉旋轉定理:
歐拉 (Leonhard Euler) 於1775年根據簡單的幾何論述證明了這個旋轉定理:
在三維空間中,若一個剛體發生位移且剛體內至少有一點固定不動(通常情況下,此固定點為原點),則此位移等價於一個繞著穿越該固定點的固定軸的旋轉。
簡單講,歐拉旋轉定理說:每一個三維空間旋轉皆可表示為對於一固定軸的旋轉。
用線性代數術語來說,若 R 是一個定義於 R3 的旋轉矩陣,則存在一非零向量 u 使得:
R u = u,
我們稱 u 是對於 R 的一個不動點(fixed point)。
幾何意義是 u 表示旋轉軸的指向向量,旋轉軸上的每一點 ku (k 是實數) 不受旋轉運動而改變。
Reference
Rotation Matrix
幾何變換矩陣的設計
三維空間的旋轉矩陣
文字內容 或 影像內容 部份參考、引用自網路,如有侵權,請告知,謝謝。
全站熱搜


 留言列表
留言列表
