正交 (Orthogonal) @ 拾人牙慧

在向量空間中，如果兩個向量內積值為0，則此兩個向量為正交，反之亦然，如果兩向量為正交，則其內積值必為0。

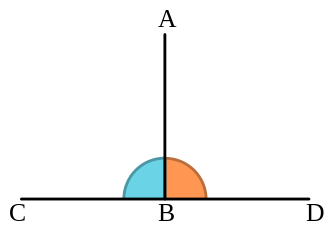
如圖，向量 AB = (0, -3)，向量 CD = (3, 0)，其內積值為 (0 x 3) + (-3 x 0) = 0，所以 AB 與 CD 為正交向量。

其他例子如：向量(1, -1) 和向量 (2, 2) 正交，其內積值為 (1 x 2) + (-1 x 2) = 0，所以這兩個向量也是正交。

在 N 維向量空間中，任何一個任意數值的向量，都可由此向量空間中的 N 個彼此正交之向量的線性組合所合成。

對於實函數而言，如果兩個實函數的內積值可定義為兩個實函數相乘後的積分，則：兩個實函數的正交，可以定義為兩個實函數相乘後的積分為 0。

Reference

Orthogonality

文字內容或影像內容部份參考、引用自網路，如有侵權，請告知，謝謝。