Pinhole Camera: Epipolar Geometry－拾人牙慧

一般來說，由兩個不同的角度來看同一個物件，其所構成的投影幾何就稱為 Epipolar Geometry。

Epipolar Geometry Model

當一個三維世界座標的點經過兩台位置不同的相機來觀看，這二台相對旋轉為 R ，相對位移為 t，且 Q 及 Q' 分別為該點相對於這兩台相機的相機座標，則 Q 及 Q' 滿足以下關係：
Q' = RQ + t

當世界座標的點被投影到這兩台相機的成像平面時，其座標位置分別為 q 及 q'，座標單位為像素(pixel)。
兩台相機的焦點所連成的直線稱為 baseline，並且穿過 (延伸) 成像平面的點為 e 及 e'，稱為 epipole；在兩台相機的相對距離不變的情況下，不管世界座標的點位在何處，epipole 的位置都不會改變。
這七個點所形成的平面稱為 Epipolar Plane (π)，和兩個相機的成像平面分別相交於 l 及 l' ，稱為 epipolar line。
epipolar_geometry

Epipolar Constraint

假設從 Camera C 來看，某一物體的點成像在 C 的影像座標為 q，則該物體在真實世界的位置一定是在 C 到 q 的這條直線上，而這條直線的投影，在另一台相機的成像平面為 epipolar line - l'，而這也暗示著，該物體的點，在第二台相機的成像上，一定會位於 l' 這條直線上，這樣的條件就稱為 epipolar constraint。

在實際的應用上，如果要在右側影像中，找尋找尋相對於左側影像的某一個 feature point，只要延著 Epipolar Line 搜尋即可，而不用尋找整張影像。
又或是如果已經有一些 Candidate 的 feature point，可以利用 Epipoloar Line 來剔除一些 Outlier。

Epipolar Constraint 在兩台相機對同一物體所投影產生的相關影像座標，可以表示為：
q'^T F q = 0
這個 3x3 的矩陣 F 稱為 Fundamental Matrix。

疑問：上述的表示法為何可以代表 Epipolar Constraint ？

解答：
如 Epipolar Geometry Model 的圖中，q̅ 及 q̅' 分別為 Q 在 C 及 C' 中的相機座標，將 q̅, q̅', C, C' 以世界座標表示為：q̅_w, q̅'_w, C_w, C'_w，則因為 Epipolor Constraint 的關係，所以此四點共平面，必定滿足：
(q̅_w - C_w)^T [(C_w - C'_w) x ((q̅'_w - C'_w)) ] = 0
其中：
x 為外積運算(Cross Product)

滿足此方程式的原因為：共平面的兩個向量作外積，其外積值會垂直此平面，則此外積值與平面中的任意向量皆為正交，故其內積值必為0。

接著，要改寫 Epipolar Constraint 的公式：

在外積的運算中，可以利用矩陣與向量相乘來取代：

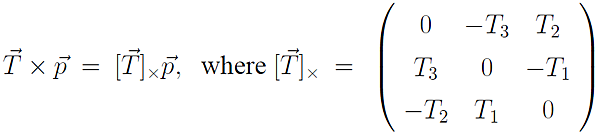
("T(T1, T2, T3) 與 P 的外積運算" 等於 "[T]_x 與 P 的矩陣-向量運算"。)

又 q̅_w - C_w = (R^L)^Tq̅，同理 q̅'_w - C'_w = (R^R)^Tq̅'。
(公式左側為兩個世界座標點的相差之值，右側為相對的兩個相機座標點的相差之值加上相機原點及世界座標原點之間的旋轉作用，所以等式會成立。)

所以上述公式可以改寫為：
q̅^TEq̅' = 0 (Epipolar Constraint)
其中 E 為 3x3 Essential Matrix (or E-matrix)：
E = R^L [C_w - C'_w]_x (R^R)^T

q̅^TEq̅' = 0 => q^T(K^-1)^T E (K^-1)q' = 0 => q^T F q' = 0

以右側的 Epipole e' 來說，可以以如下算式表式：
e'_c = αM_ex^R[(C_w)^T, 1]^T = αR^R(C_w -C'_w)
其中：
M_ex^R = (R^L -R^LC_w)
α 為非零常數

上述的算式會成立的原因在於如果以 C' 為原點，則 Epipole e' 必定會存在於 C' 與 C 相連的直線上。

接著將上述座標點，套用到 Epipolar Constraint 的算式：
q_c^T E e'_c = α(q_c)^T R^L [C_w - C'_w]_x R^R(C_w -C'_w) = 0

所以，可以証明該 Epipole 存在於每條 Epipolar Line。

假設這兩台相機的內部參數都一樣，則上式可以再表示為：

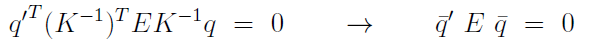
矩陣 E 稱為 Essential Matrix。
K^-1q 及 K^-1q' 的作法是為了將影像座標 q 及 q'，還原為相機座標。

Fundamental Matrix F 包含著內部參數的資訊，直接與兩台相機的影像座標有關聯；然而，Essential Matrix E 為相機座標之間的矩陣關係，而如之前所述這兩台相機的位置關係可以相對旋轉 -R 及相對位移 -t 表示，所以 E 可以定義為：

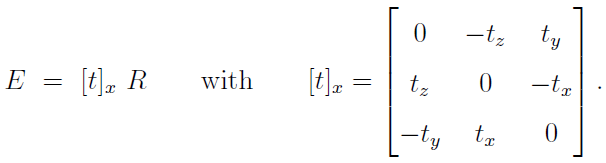
矩陣 [t]_x 為位移向量 t = [t_x, t_y, t_z]^T 的斜對稱矩陣，這表示 E 可以被用來重建兩個 camera 之間的位置關係，因為可以單獨分解出 rotation 及 translation 的關係。

疑問：求出 E 之後，該如何分解 E 矩陣？

Epipolar Geometry 的缺陷

Essential Matrix 的 rank 為 2，所以它只有 5 個 degrees of freedom：rotation 有 3 個，translation 有 2 個，因此在兩個影像之間，其位移的 scale 並無法被確定。

疑問：什麼是矩陣的 degree of freedom？上述這段話又是在說什麼？

實際應用上，很多問題隨著使用 Essential Matrix 而產生，因為 Epipolar Geometry Model 並不適用於相機之間只有單純旋轉的情況，猜測原因為：因為無法畫出 Epipolar Plane；而 Epipolar Geometry Model 也不適用於拍攝同一平面的物體，在這兩種情況下，需要 Homography Model 來求相機之間的相對位移及旋轉。

疑問：為什麼 Epipolar Geometry Model 不適用於拍攝同一平面的物體？

Pinhole Camera 相關文章：
相機座標成像原理
相機校正 (Camera Calibration)
3D 深度預測 (3D Depth Estimation)
Epipolar Geometry
Homography

Reference

Visual Odometry on Mobile Devices for Virtual Walkthroughs
Epipolar Geometry

文字內容或影像內容部份參考、引用自網路，如有侵權，請告知，謝謝。